 Índice ÓRBITAS DE SATÉLITE DA
TERRA
Índice ÓRBITAS DE SATÉLITE DA
TERRA
-
De acordo com a primeira lei
de Kepler, toda órbita é uma cônica (circulo, elipse,
parábola, hipérbole) onde a Terra ocupa um dos focos. Nas
duas ultimas, o satélite só passa uma vez perto da Terra.
Nos interessam as órbitas circular e elíptica. O circulo é
apenas um caso particular de elipse com excentricidade e = 0, ou seja,
os focos ocupam o mesmo lugar no centro do circulo.
-
Segunda lei de Kepler : o raio
r varre áreas iguais em tempos iguais. Portanto, a velocidade
do satélite é mínima no apogeu e máxima no
perigeu.
-
Terceira lei de Kepler ( lei harmônica
) : o quadrado do período de revolução P é
proporcional ao cubo do semi-eixo maior a : P² = a³ ( 4 p
² / m ) ,
onde m = G M
e G = constante gravitacional universal = 6,673 . 10–11 Nm²
/ kg² , M = massa da Terra = 5,98 . 1024 kg e P = período em segundos.
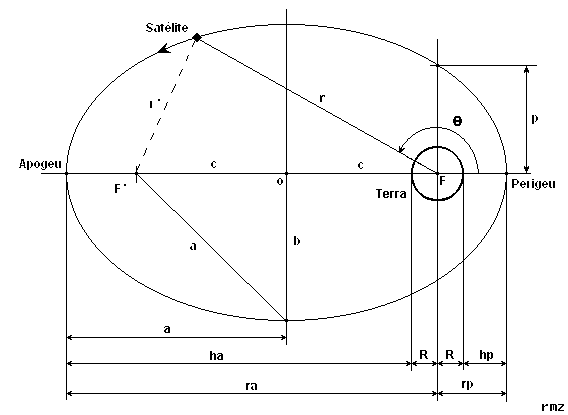
Propriedades básicas da órbita elíptica
(ou circular para e=0):
|
a = semi-eixo maior
|
b = semi-eixo menor
|
|
c = meia distancia
entre focos F e F’ c = a e
|
a² = b² + c²
|
|
e = excentricidade e =
c / a = (ra - rp) / (ra + rp)
|
p = semi lado reto p = a ( 1
- e² )
|
|
r = raio do satélite
ao centro da terra
|
R = raio da Terra = 6378 km ( no equador )
|
|
r = p / ( 1 + e cos q
) |
q
= anomalia verdadeira |
|
rp = raio do perigeu = a ( 1
- e )
|
ra = raio do apogeu = a ( 1
+ e )
|
|
ra + rp = 2 a
|
a = r + r ‘ = constante
|
|
hp = rp – R = altura do satélite
no perigeu
|
ha = ra – R = altura do satélite
no apogeu
|
O programa RZ3
permite simular em escala exata diversas órbitas de satélites da
terra, permitindo alterar interativamente parâmetros como excentricidade,
altura do apogeu e perigeu etc...
Calcula o período e a velocidade
em diversos pontos da órbita e mostra em escala a velocidade relativa do
satélite na sua órbita (visualizando a segunda lei de Kepler).
ELEMENTOS ORBITAIS ( KEPLERIANOS
)
Exemplo de dados keplerianos no formato 2 linhas
(NASA):
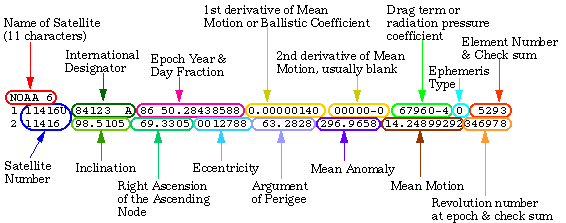
Os elementos básicos que definem
a órbita de um satélite são :
-
Época : instante de tempo de especificação
dos valores dos elementos (Epoch Year & Day Fraction))
-
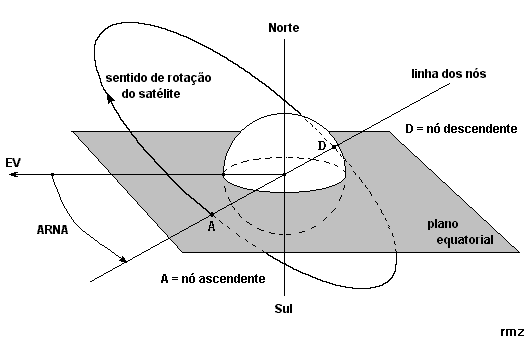
Inclinação orbital : angulo
entre o plano da órbita e o plano equatorial (Inclination)
-
ARNA : ascensão reta do nó
ascendente ( em relação ao equinócio vernal ) Em inglês:
RAAN (Right Ascension of the Ascending Node)
-
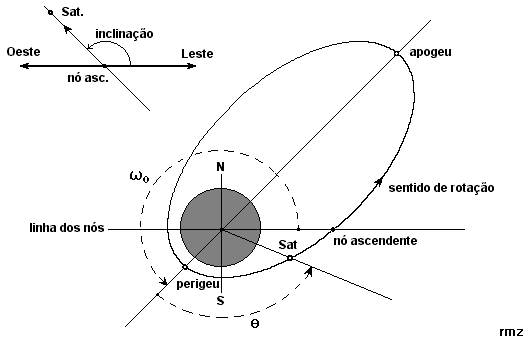
Argumento do perigeu : w
0 (Argument of Perigee)
-
Excentricidade : 0 <= e < 1 (Exccentricity)
-
Movimento médio : quantidade de
revoluções por dia (Mean Motion)
-
Anomalia média : posição
do satélite na órbita ( 0° a 360°, 0° = perigeu)
(Mean Anomaly)
-
Arrasto : razão de mudança
do movimento médio (Ballistic Coefficient)
ÓRBITA GEOESTACIONÁRIA
GSO
Para que o satélite permaneça
numa posição fixa em relação a um ponto na
Terra, é preciso que esteja em uma órbita geoestacionária GSO, com as seguintes características :
-
a órbita deve ser geossíncrona GEO, ou seja,
ter o mesmo período de revolução da Terra, que é
de um dia sideral = 23 h 56 mn 04s. Portanto, devera ter semi-eixo maior
de 42164 km.
-
a órbita deve ter excentricidade zero,
ou seja, deve ser circular. O semi-eixo maior é o raio r da órbita.
A altura do satélite será portanto de 42164 - 6378 = 35786
km
-
a órbita deve ter inclinação
zero, ou seja, o satélite deve girar no plano do equador e no mesmo
sentido da rotação da Terra.
Obs: Toda órbita geoestacionária GSO é também
geossíncrona GEO, mas nem toda GEO é GSO !
Veja aqui um exemplo de órbita
geossíncrona.
ÓRBITA
DE TRANSFERÊNCIA GEOESTACIONÁRIA
A GTO é uma órbita elíptica
com perigeu aproximado de 500 km onde a velocidade é de 35940 km/h,
e apogeu de 35786 km onde a velocidade é de 5860 km/h. A partir
de Kourou por exemplo, esta órbita tem uma inclinação da
ordem de 7 graus. No apogeu é ligado um motor para aumentar a velocidade
para 11069 km/h e obter a órbita circular GEO (geossíncrona). É feita também
uma correção na inclinação para que seja zerada e
obter assim uma órbita GSO
(geoestacionária)
PERÍODO E VELOCIDADE DE SATÉLITE
EM ÓRBITA CIRCULAR
P2 = 4 p2
r 3 / G M
V = ( G M / r )½
r = raio do satélite ao
centro da Terra r = R + h
P = período em segundos
h = altura do satélite
G M = 3,986.1014 m³
/ s²
R = raio da Terra = 6378 km ( no equador )
| h
( km ) |
V
( km / h ) |
Período |
Observações |
| 1 |
28547 |
1
h 24 mn 30 s |
* |
| 100 |
28238 |
1
h 26 mn |
* |
| 300 |
27813 |
1
h 30 mn |
ISS |
| 1700 |
25446 |
2
h |
- |
| 6400 |
20106 |
4
h |
- |
| 20240 |
13930 |
12
h |
GPS |
| 35786 |
11069 |
23
h 56 mn 04 s |
GEO |
| 380000 |
3650 |
654
h |
Lua |
-
* Na tabela acima a altura de 1 km só
seria possível sem atmosfera e sem montanhas !...Consta apenas para
se ter uma idéia do limite mínimo do período e da
velocidade mínima para colocar um satélite em órbita. Mesmo
a altura de 100 km é impraticável por causa do efeito de
atrito da atmosfera. A estação espacial internacional ISS
fica entre 350 e 400 km aproximadamente.
-
A ultima linha corresponde aproximadamente
a órbita da Lua (que na verdade é ligeiramente elíptica.
Veja no programa RZ3 ).
-
Para efeito de comparação,
a velocidade de escape da Terra = ( 2 G M / R )½
= 40248 km/h, é a velocidade para escapar do campo gravitacional
da Terra, ou seja, não permanecer mais em órbita da Terra.
 Índice
Índice




