Satélite diferente ?... Nem tanto! Mas interessante !
Você já viu um satélite cujo movimento
aparente (rastro terrestre) tem a forma de um "8" ?
Elaborei os keplerianos de um satélite assim, que batizei de PY4ZBZ-1 (dowload aqui):
1 99999U 06001A 06070.01234321 -.00000000 00000-0 00000+0 0 0015
2 99999 60.0000 219.0000 0000000 060.0000 210.0000 1.00273000 0018
Veja o seu rastro terrestre (ground track) em forma de "8" nas figuras seguintes, feitas com o Orbitron (curva amarela).(a curva verde é o footprint visual do satélite na posição em que está na figura, ou seja, no meio do 8). Lembramos que o rastro terrestre da órbita de um satélite é o caminho percorrido pelo SSP do satélite na superfície da terra (SSP=Sub Satellite Point, ponto na superfície da terra e na vertical do satélite). O rastro terrestre é totalmente diferente da própria órbita, que é sempre uma elipse (primeira lei de Kepler) cuja excentricidade é um valor entre zero e menor que 1. Caso a excentricidade seja zero, a elipse vira um circulo, que é apenas um caso particular de elipse. O rastro terrestre é a combinação de dois movimentos: o do satélite na sua órbita com a rotação da terra !
Use os keplerianos no seu programa de rastreamento de satélites e veja detalhes como características da órbita e o rastro terrestre.
Faço as seguintes perguntas:
1 - Qual é o tipo de órbita desse satélite ? (LEO,GEO,Molnya,etc...)
2 - Porque o ground track tem a forma de um "8" ?
3 - Como é chamada esta figura em forma de "8" ?
Respostas :
A figura seguinte (NASA) mostra resumidamente o significado dos dados keplerianos (mais detalhes aqui):
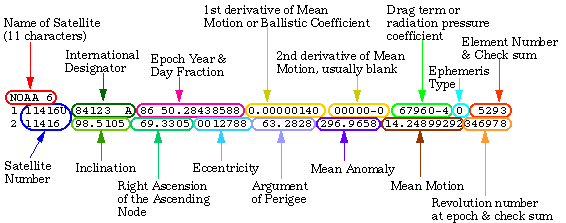
Resposta 1:
a - Nos keplerianos, vemos que a excentricidade da órbita é zero. Portanto, se trata de uma órbita perfeitamente circular, onde a velocidade do satélite e a sua altura são constantes.
b - Os keplerianos nos informam também que o movimento médio é de 1,00273 revoluções por dia, o que permite deduzir um período de 24 h / 1,00273, o que equivale a 23 horas, 56 minutos e 04 segundos, ou seja, um dia sideral, que é exatamente o tempo que a terra leva para rodar 360 graus (uma volta) em torno do seu eixo ! Não confundir com o dia solar, que é de 24 horas, e é o tempo que a terra leva para reapresentar o mesmo meridiano de frente para o sol ! Para tal, ela precisa dar um pouco mais de 360 graus, pois enquanto gira em torno do seu eixo, também gira mais 360/365,2425=0,9856 graus em torno do sol (translação) e no mesmo sentido, tendo que girar 360,9856 graus para completar um dia solar.
c - Os keplerianos também indicam que a inclinação da órbita é de 60 graus. Portanto, como é menor que 90 graus, o satélite gira no mesmo sentido da rotação da terra. Como esta órbita está em sincronismo com a rotação da terra (mesmo período e mesmo sentido), é chamada de GEO ou geossíncrona. Se a sua inclinação fosse exatamente zero, e somente nesse caso, ela seria também GSO = geoestacionária, que significa que o SSP do satélite está sempre no mesmo lugar da terra, em cima do equador. É o caso da maioria dos satélites de TV, para os quais a antena terrestre tem apontamento fixo. A órbita GSO é apenas um caso particular de órbita GEO, mas muitíssimo usada na pratica: é no famoso cinturão de Clarke que ficam os satélites GSO.
d - Existem muitos satélites GEO em órbita da terra, a maioria sendo satélites que eram GSO (tinham inclinação zero) e foram retirados do cinturão de Clarke, no final de sua vida, para dar o precioso e caríssimo lugar a outro satélite GSO novo. Um exemplo de GEO é o Brasilsat A1. A única diferença para o PY4ZBZ-1 é que tem inclinação muito menor, geralmente menor que 10 graus. E na verdade até todos os GSO (geoestacionários) também tem um ground track em forma de um pequeníssimo 8, pois não estão EXATAMENTE com inclinação zero, devido ao erro de posicionamento, que quando ultrapassa um certo limite (da ordem de 0,1 grau) é recolocado mais próximo possível da posição correta de longitude e com inclinação mais próxima de zero possível, usando motores apropriados. Se o 8 é menor que a largura de feixe da antena terrestre, esta pode ter apontamento fixo. Caso contrario, a antena terrestre deve seguir o 8, que é percorrido uma vez por dia, por meio de um sistema de rotores azimute/elevação automatizado.
Resposta 2:
O rastro terrestre (ground track) é a combinação de dois movimentos: o do satélite na sua órbita em volta da terra, com a rotação da terra dentro da órbita do satélite ! Toda órbita é uma elipse, com um dos focos situado no centro da terra.
A figura seguinte ajuda entender porque, apesar da velocidade e altura constante do satélite em uma órbita perfeitamente circular = elipse com excentricidade zero, o rastro terrestre do seu SSP tem uma forma de "8":
A parte esquerda da figura é uma vista de muito longe e de cima do pólo norte da terra (circulo azul). Mostra uma órbita GSO que portanto é vista como um circulo, e uma órbita GEO, inclinada de 60 graus, que portanto é vista como uma elipse com semi-eixo menor co-seno de 60 graus = 0,5 vezes menor que o seu raio (a órbita na verdade também é circular, mas não está de frente para o observador como no caso da GSO).
Como a terra e os satélites GSO e GEO tem exatamente a mesma velocidade de rotação, o SSP do GSO estará sempre em cima do mesmo ponto e no equador da terra, com longitude constante, e latitude zero. Mas o SSP do GEO só está com a mesma longitude do GSO nos pontos 1, 3, 5 e 7. Somente nos pontos 1 e 5 o SSP do GEO é o mesmo do GSO.
E nos pontos 3 e 7, tem a mesma longitude mas com latitude positiva ou negativa igual a inclinação i da órbita.
A posição instantânea ou movimento no sentido vertical (latitude) do SSP é uma função senoidal do angulo w do satélite na sua órbita:
Lat SSP = i.sen(w)
Podemos ver na figura que, por exemplo, para w=45 graus (ponto 2' ), a longitude do SSP do GEO está atrasada em relação a longitude do GSO, de um angulo d = a-w. Na figura podemos deduzir o valor do angulo a , sendo R o raio da órbita e i a sua inclinação :
x=R.sen(w) y=x.cos(i) c=R.cos(w) tg(a)=y/c=Rsen(w).cos(i) / Rcos(w)=cos(i).tg(w)
e finalmente : a = atn ( cos(i). tg(w) )
Por exemplo, para i = 60 graus e w = 45 graus, a = 26,565 graus. Portanto, o SSP está atrasado em d=45-26,565=18,435 graus em relação ao ponto 1. (no sentido da rotação da terra)
Este valor d pode ser perfeitamente conferido na figura anterior a direita, feita com o Orbitron, e usando como referencia a escala de longitudes !
No ponto 4 ocorre algo semelhante, só que agora o SSP está adiantado do mesmo valor absoluto de 18,435 graus.
E tudo se repete nos pontos 6 e 8 respectivamente.
A figura desenhada pelo SSP nada mais é que uma figura de LISSAJOUS, ou seja, a composição em dois eixos ortogonais x e y de duas funções periódicas, harmônicas ou não. No caso desse satélite temos duas funções harmônicas, x tendo o dobro da freqüência de y:
y = i.sen(w) e x = atn ( cos(i). tg(w) ) - w
Para w variando de 0 a 360 graus, a função y faz um ciclo (senoidal) e a função x tem dois ciclos idênticos (mas não senoidais), cuja composição em eixos ortogonais é a figura do 8, e cujo período é de um dia sideral, ou seja, o SSP percorre todo o 8 em um dia sideral ou 23horas 56minutos 04segundos. Isso pode ser verificado facilmente no Orbitron no modo simulação.
A figura seguinte mostra o gráfico exato da variação da latitude e longitude do SSP para uma inclinação de 60 graus (O fator1/2 nada mais é que co-seno de 60). A variação de latitude é sempre senoidal, mas a variação de longitude não ! :

A figura seguinte mostra o principio da composição destes dois movimentos ou funções:

Resposta 3:
Se plotarmos (ou fotografarmos) a posição do sol todos os dias (ou outro intervalo qualquer múltiplo inteiro de dias) durante um ano, mas sempre no mesmo horário, para cancelar o efeito da rotação da terra, e com a maquina fotográfica sempre na mesma posição e sem mudar o filme, teremos uma figura parecida, principalmente se fizermos isso num ponto da terra situado no equador, onde o "8" será visto com mais simetria. Esta figura é chamada de ANALEMA:
O formato do analema é devido a duas coisas:
1 - o fato do eixo da terra ser inclinado 23,5 graus em relação ao sol (a "altura do 8" é proporcional a esta inclinação), da mesma forma que para o satélite GEO é devido a inclinação da sua órbita : a altura (latitude máxima + e -) de cada laço é exatamente igual a inclinação da órbita se esta for circular, e a altura pico a pico é sempre o dobro da inclinação, para órbitas elípticas, como mostrado a seguir.
2 - O fato da órbita da terra em torno do sol não ser circular, mas ligeiramente elíptica (e = 0,017), é a causa da largura dos laço do analema, e causa uma não simetria dos laços do "8" do satélite, como pode ser visto na foto de um analema abaixo e nas figuras seguintes, onde o satélite PY4ZBZ-2 continua com inclinação i = 60 graus (=máximas latitudes do SSP), mas com excentricidade e = 0,1 , e o satélite PY4ZBZ-3 com e = 0,3. A largura dos laços no caso do satélite é devida ao fato de que a projeção da sua órbita, mesmo sendo circular, sobre o plano equatorial, é uma elipse, como mostrado anteriormente.
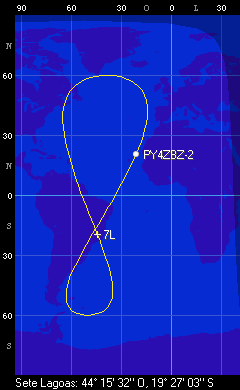

O analema (do sol) nada mais é que uma projeção semelhante ao SSP de um satélite GEO, porém considerando o sol como satélite da terra, como se pensava antigamente ... o resultado sendo o mesmo com a terra girando em torno do sol ! Apenas, no caso do sol, é preciso excluir a rotação da terra em torno do seu eixo, para que seja levado em consideração somente a translação da terra em torno do sol.
E para quem ainda duvida se a figura é um analema, compare as formas do rastro terrestre do PY4ZBZ-4 (keps aqui), que é um satélite com inclinação orbital igual a do eixo da terra : i = 23,5 graus e com a mesma excentricidade da terra e = 0,017, com a foto real do analema ! (a orientação do analema depende de fatores como latitude do local e horário da observação)
Uma diferença entre o analema solar e o do satélite é que o solar é feito de pontos (no Maximo 365 pontos, um por dia, durante um ano) enquanto o satélite GEO descreve realmente uma curva continua.
A figura animada seguinte mostra um exemplo de orbita GEO dos satélites Sirius:
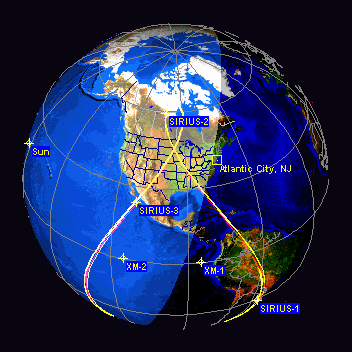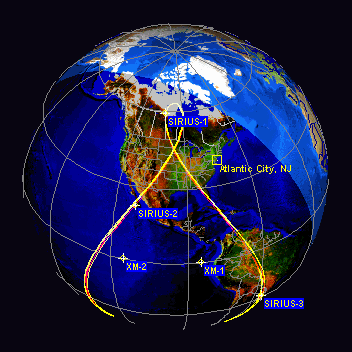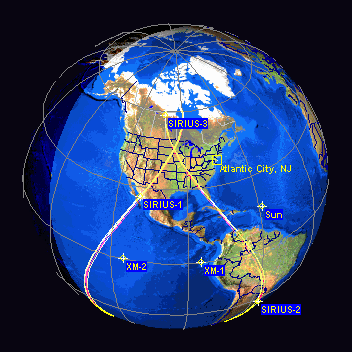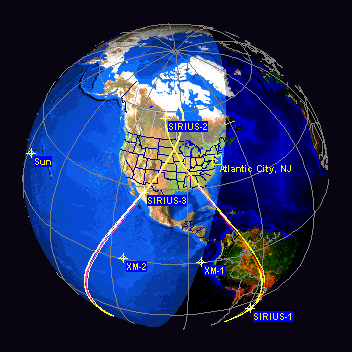
Satélites Sirius vistos no Orbitron:

Obs. : No meu artigo sobre analema, usei as mesmas abreviações da Celestrak, para GSO e GEO, GeoStationary orbit GSO e GEOsynchronous orbit GEO que são INVERTIDAS em relação ás usadas pela maioria de outros autores ! : GeoSynchronous Orbit GSO e Geosynchronous Equatorial Orbit GEO.
Mais links:
http://www.perseus.gr/Astro-Solar-Analemma.htm
http://en.wikipedia.org/wiki/Analemma
Como fotografar um analema 1 e 2
Por PY4ZBZ em 14-03-2006, rev 12-07-2015.