Por PY4ZBZ em  25-03-2001.  rev.  14-02-2007

Onda com modulação angular, vista em "câmera lenta".

Definições básicas.

• Modulação : variação de um parâmetro de uma onda portadora senoidal, de maneira linearmente proporcional ao valor instantâneo do sinal modulante ou informação.
• Portadora : Onda senoidal que, pela modulação de um dos seus parâmetros, permite a transposição espectral da informação (ou sinal modulante).
• Como a portadora senoidal tem três parâmetros : Amplitude, Freqüência e Fase, existem três formas básicas de modulação : Modulação em Amplitude AM,   Modulação em Freqüência, FM  e Modulação em Fase, PM.

Definições de FM e PM.

Observação importante: é impossível modular uma onda em freqüência (FM) sem provocar variações na sua fase, assim como não é possível modular uma onda em fase (PM) sem causar variações na sua freqüência, porque a freqüência é proporcional a derivada da fase :

f = (1/2p) dF/dt

 Por isso, FM e PM são chamadas modulações angulares. Muita gente confunde FM com PM, que apesar de certas semelhanças, são dois tipos de modulação bem diferentes, como mostrarei a seguir.

Consideramos o sinal modulante como sendo uma senóide: 

  vm(t) = Vm sen (2 p fm t). 

(O caso de um sinal modulante complexo será considerado mais adiante).

FM:  Uma onda modulada em freqüência (FM) tem freqüência instantânea linearmente proporcional ao valor instantâneo do sinal modulante. Portanto, uma onda FM sofre diretamente desvios de freqüência, e que são:

O desvio de freqüência de pico  df  da onda FM é proporcional (pela constante k_f ) ao valor de pico Vm (ou amplitude) do sinal modulante: 

df = k_f Vm.

O desvio de freqüência instantâneo  df(t)  da onda FM é proporcional (pela constante k_f ) ao valor instantâneo vm(t) do sinal modulante: 

df(t) = k_f vm(t).

Portanto, a onda FM é:   vp(t) = Vp sen [ 2 p ( fp + df(t) ) t ]

Ou ainda:    vp(t) = Vp sen [2 p fp t - (k_f / (2 p fm) ) Vm cos (2 p fm t)]       (1)

Uma onda modulada em freqüência, difere de uma onda pura, no fato de que a sua fase sofre uma variação proporcional a integral do sinal modulante.

PM:  Uma onda modulada em fase (PM) tem fase instantânea linearmente proporcional ao valor instantâneo do sinal modulante. Portanto, a onda PM sofre diretamente desvios de fase, que são:

O desvio de fase de pico dF  de uma onda PM é proporcional (pela constante k_p ) ao valor de pico Vm (ou amplitude) do sinal modulante:

dF = k_p Vm

O desvio de fase instantâneo dF(t)  de uma onda PM é proporcional (pela constante k_p ) ao valor instantâneo vm(t) do sinal modulante:

dF(t) = k_p vm(t)

Portanto, a onda PM é:   vp(t) = Vp sen (2 p fp t + dF(t) )

A freqüência instantânea da onda modulada em fase é proporcional a derivada do sinal modulante:

   f(t) = fp + k_f fm Vm cos (2 p fm t)       (2)

Tanto em  FM como em PM, a amplitude Vp da onda modulada é CONSTANTE.

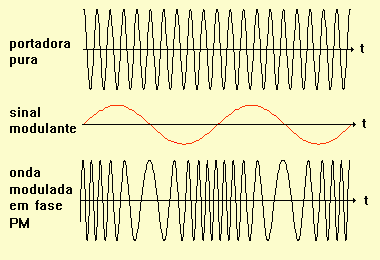
A figura seguinte mostra a relação entre portadora pura, sinal modulante e a onda FM :

É possível demonstrar matematicamente, que uma onda MODULADA em freqüência, FM (que por definição tem freqüência instantânea linearmente proporcional ao valor instantâneo do sinal modulante), sofre também variações de fase proporcionais a integral do sinal modulante. (equação 1 acima) Isso confirma a observação importante do inicio deste texto.

É muito importante distinguir os termos MODULAÇÃO e VARIAÇÃO !

Portanto, uma onda modulada em fase, PM, (que tem por definição fase instantânea linearmente proporcional ao valor instantâneo do sinal modulante) sofre também variações de freqüência proporcionais a derivada do sinal modulante (equação 2 acima), como se vê na figura seguinte (bem diferente da anterior !) :

Banda ocupada. 

Teoricamente, uma onda FM ou PM é composta de uma infinidade de ondas senoidais de freqüências fixas (raias), simétricas em relação a freqüência da portadora fp, eqüidistantes, separadas pelo valor de fm, a freqüência do sinal modulante.
Na pratica, felizmente, as raias acima de uma certa ordem podem ser desprezadas por serem muito pequenas. Desprezando as raias com menos de 10% de amplitude (em tensão, o que equivale a 1% em potência) em relação a portadora pura, a banda ocupada em FM ou PM é dada pela formula de Carson :

 B = 2 ( df + fm max ) = 2 ( n + 1 ) fm max

onde dpf é o desvio de freqüência de pico da onda FM,  fm max é a máxima freqüência do sinal modulante, e n o índice de modulação.

Um parâmetro importante em FM ou PM é o índice de modulação  n, definido a seguir: 

n = df / fm = dF.

Porque n define o nível das raias ou sinais senoidais que compõem a onda FM ou PM.
As funções de Bessel permitem obter o valor de cada raia em função de índice de modulação n.  A figura seguinte mostra o valor da portadora (raia J0) e das quatro primeiras raias laterais (J1 a J4) :

A figura seguinte mostra o espectro de uma onda FM ou PM e o respectivo desvio de freqüência pico a pico = 2df da onda FM ou PM, para diversos valores do índice de modulação n , que é igual ao desvio de fase (em radianos) : Na figura acima, para n = 2 por exemplo, podemos ver 10 raias laterais (5 de cada lado da portadora). Porém, o nível da quarta e quinta raia é menor que 0,1 (10%) (ver gráfico das funções de Bessel), portanto desprezíveis.
Consequentemente e apesar do desvio de freqüência ser de 4fm pico a pico, a banda ocupada é de 6fm, confirmando a lei de Carson.
Observa-se também que a raia com freqüência da portadora tem nível menor que a portadora pura, podendo até se anular, por exemplo para n = 2,4 e 5,5, pontos chamados de Bessel-zero.
A figura seguinte é o espectro do primeiro Bessel-zero da portadora, com n = 2,405 e
fp = 2000 Hz, fm = 200 Hz, df = 481 Hz e B = 1362 Hz (nível da portadora pura: -10 dB). Também ocorrem Bessel-zero para as raias laterais.
Numa onda FM ou PM , o somatório da potência de todas as raias é constante e igual a potência da portadora pura, ou seja, a amplitude da onda FM ou PM é constante. (independente de n) .

As 7 figuras seguintes mostram exatamente as formas de onda e espectros de um sinal FM, para diversos índices de modulação n (nas figuras m). A primeira mostra o sinal modulante com freqüência f:

A segunda mostra a portadora pura, com freqüência 6f (6 vezes a freqüência do sinal modulante):

A terceira mostra um sinal FM com n=0,5:

A quarta mostra um sinal FM com n=1:

A quinta mostra um sinal FM com n=2 :

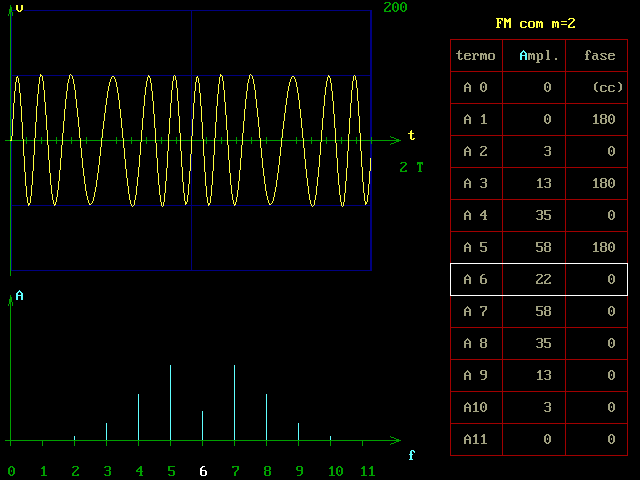
A sexta mostra um sinal FM com n=2,4 (primeiro Bessel-zero da portadora) :

A sétima mostra um sinal FM com n=3,8 (primeiro Bessel-zero da 1a raia lateral) :

Estas 7 figuras anteriores foram feitas com o programa didático RZ1 (download aqui).

Composição vetorial da onda com modulação angular.

A figura seguinte mostra como o somatório da portadora com as raias laterais resulta em uma onda com amplitude constante R e fase variável. São mostrados 5 instantes diferentes, marcados de 1 a 5 (em verde). No caso, as amplitudes relativas da portadora J0 (0,77) e das raias laterais J1 (0,44), J2 (0,11), J3 (0,02) superiores e inferiores correspondem exatamente a um índice de modulação n=1. Como o índice de modulação equivale ao desvio de fase de pico, observamos um desvio de fase de 1 radiano da onda resultante R, nos instantes 1 e 5, sendo que o instante 3 mostra a resultante R com a fase de referencia, idêntica a da portadora. Como o somatório vetorial é sempre constante e igual a amplitude da onda resultante R , este vetor R tem como lugar geométrico um circulo:

Até agora, usamos como sinal modulante uma simples senóide. O que acontece quando o sinal modulante for uma onda complexa, como um sinal de áudio ou vídeo ?
É simples : o sinal modulante complexo é constituído de uma certa quantidade de ondas senoidais (raias) (Teorema de Fourier). Para cada uma destas raias do sinal modulante teremos um espectro do sinal FM ou PM como foi visto acima, com diversas raias laterais. O sinal FM ou PM resultante é o somatório de todos eles, tornando-se um sinal com espectro bastante complexo.

Obs: não é possível saber se uma onda é FM ou PM apenas pela sua forma de onda ou pelo seu espectro : é preciso ter como referencia, para a forma de onda, o sinal modulante. Ou ainda, é preciso poder mudar a freqüência do sinal modulante sem variar a sua amplitude e observar o efeito no espectro: se o aspecto do espectro, como quantidade e amplitude relativa das raias, permanecer constante, mudando apenas o espaçamento das raias, trata-se de um onda modulada em fase PM, pois o índice de modulação n permaneceu constante. Em PM, o índice de modulação depende apenas da amplitude do sinal modulante. Em FM, o índice de modulação também é diretamente proporcional a amplitude do sinal modulante, mas além disso ainda é inversamente proporcional a freqüência do sinal modulante.

Conseqüências praticas da diferença entre FM e PM.

Na pratica, uma onda só pode ser modulada diretamente em FM no oscilador onde é gerada, variando-se um dos parâmetros L ou C do circuito oscilante. Em estágios posteriores ao oscilador, não é mais possível modular diretamente em freqüência, mas é perfeitamente possível modular o sinal em fase. Se quisermos uma onda modulada em FM, num estagio apos o oscilador, usamos um modulador de fase, e aplicamos a operação matemática de integração ao sinal modulante, como mostra a figura seguinte:

Inversamente, podemos gerar uma onda modulada em fase (sem usar um modulador de fase) usando um modulador de freqüência, e tendo o cuidado de aplicar a operação de derivação ao sinal modulante, como mostra a figura seguinte:

Estes recursos são muito usados na pratica, principalmente quando queremos uma onda FM, com 6dB por oitava de pré-ênfase. A pré-ênfase com razão de 6 dB por oitava é equivalente matematicamente à derivada do sinal modulante, o que pode ser obtido com um simples circuito RC. Portanto, podemos obter um sinal de FM com 6 dB por oitava de pré-ênfase usando um modulador de fase PM e mais nada ! como mostra a figura seguinte:

O circuito anterior é equivalente ao seguinte (já mostrado anteriormente com menos detalhes):

A derivada do sinal modulante o transforma em um sinal cuja amplitude passa a ser proporcional a sua freqüência, e ainda é defasado 90 graus para frente em relação ao original. 

Pois a derivada de sen(a) é  a cos(a).

No caso da pré-ênfase, na verdade só interessa o fato da amplitude ser proporcional a freqüência. A utilidade da pré-ênfase só pode ser entendida pelo estudo da demodulação do ondas FM na presença de ruído, o que não é do escopo deste artigo. Um circuito muito usado para pré-ênfase é o circuito derivador RC, que só age como derivador em freqüências abaixo da freqüência de corte fc. Nestas freqüências, o sinal de saída vs também é defasado 90 graus para frente do sinal de entrada ve :

Conclusão interessante sobre FM e PM : Quando pretendemos modular uma portadora em freqüência (ou fase), a intenção é também manter a sua amplitude constante. No entanto,  a amplitude da portadora varia com o índice de modulação e a sua freqüência permanece fixa em fp. E aparecem novos sinais senoidais, as raias laterais, que somados (vetorialmente) a nova portadora com amplitude menor que a portadora pura, resultam em um sinal complexo, modulado em freqüência (ou fase), e com amplitude constante!
Portanto, não é a portadora que é modulada em FM ou PM, mas a onda composta ou complexa resultante do somatório da portadora com as raias laterais.(veja a conclusão semelhante em AM...)

Sintese FM : O fato de que com apenas duas ondas senoidais (a portadora fp e o sinal modulante fm) é possível gerar uma quantidade enorme de sinais (as raias resultantes da modulação em FM de fp por fm) foi aproveitado na geração sintética de sons complexos, imitando os mais diversos instrumentos musicais ou vozes, chamada Síntese FM, e usada em placas de som para PC e instrumentos musicais eletrônicos.

Bibliografia:

Vejam aqui um excelente artigo da HP sobre AM e FM: o Application Note AN 150-1.

  Índice