 Índice
Índice
DIGITALIZAÇÃO DE UM SINAL ANALÓGICO
Para digitalizar um sinal analógico, são necessárias
no mínimo quatro etapas :
- Filtragem anti-aliasing.
- Amostragem : divisão do sinal no
eixo do tempo em amostras analógicas discretas PAM.
- Quantização : divisão
do sinal PAM no eixo de tensão em valores discretos finitos.
- Codificação destes
valores em bits.
Obs. : na pratica, a amostragem, a quantificação e a codificação
podem ser feitas por um único circuito eletrônico, e não
necessariamente nesta ordem, ou até simultaneamente. Para efeitos
didáticos, inclusive para distinguir bem aliasing de erro de quantização,
analisaremos cada etapa separadamente, pois são funções
bem distintas.
Filtragem anti-aliasing :
De acordo com o Teorema de Nyquist, a quantidade de amostras
por unidade de tempo de um sinal, chamada taxa ou freqüência
de amostragem, deve ser maior
que o dobro da maior freqüência contida no sinal a ser amostrado,
para que possa ser reproduzido integralmente sem erro de aliasing.
A metade da freqüência de amostragem é chamada freqüência
de Nyquist e corresponde ao limite máximo de freqüência
do sinal que pode ser reproduzido. Como não é possível
garantir que o sinal não contenha sinais acima deste limite ( distorções,
interferências, ruídos, etc...), é necessário
filtrar o sinal com um filtro passa baixo com freqüência de
corte igual (ou menor) a freqüência de Nyquist, ou filtro anti-aliasing.
O aliasing e seu efeito nocivo será
explicado oportunamente.
Amostragem do sinal :
Como o sinal analógico é continuo no tempo e em nível,
contem uma infinidade de valores. E como o meio de comunicação
tem banda limitada, somos obrigados a transmitir apenas um certa quantidade
de amostras deste sinal, como enunciado anteriormente no Teorema de Nyquist.
É obvio que quando maior a freqüência de amostragem,
mais fácil será reproduzir o sinal, mas haverá desperdício
de banda ocupada sem nenhuma melhoria na qualidade.
As figuras seguintes ilustram o principio da amostragem :
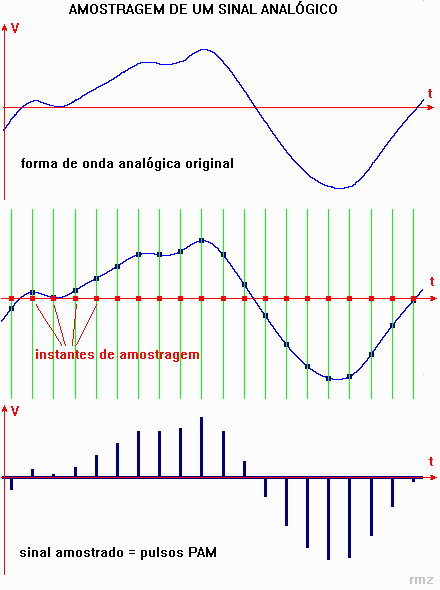 O circuito que permite amostrar o sinal é uma simples chave que
se fecha por um brevíssimo instante, na cadencia da freqüência
de amostragem. Por ex. se a freqüência de amostragem for de
8 kHz, a chave se fecha 8000 vezes por segundo, ou seja, a cada 125 micro
segundo. Como a chave se fecha por um tempo extremamente curto, teremos
na sua saída um sinal em forma de pulsos estreitos, com amplitude
igual ao valor instantâneo do sinal, chamados pulsos PAM (pulsos
modulados em amplitude)
O circuito que permite amostrar o sinal é uma simples chave que
se fecha por um brevíssimo instante, na cadencia da freqüência
de amostragem. Por ex. se a freqüência de amostragem for de
8 kHz, a chave se fecha 8000 vezes por segundo, ou seja, a cada 125 micro
segundo. Como a chave se fecha por um tempo extremamente curto, teremos
na sua saída um sinal em forma de pulsos estreitos, com amplitude
igual ao valor instantâneo do sinal, chamados pulsos PAM (pulsos
modulados em amplitude)
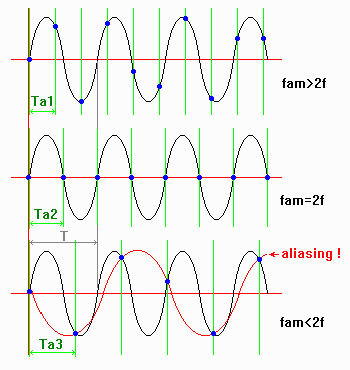
A figura seguinte mostra um sinal senoidal sendo amostrado com taxas
próximas ao limite.
Em cima, amostragem com freqüência maior que duas vezes
a do sinal : ha amostras suficientes para que o sinal possa ser reproduzido
sem erro de aliasing. (lembramos que fam = 1 / Ta)
No meio, a taxa de amostragem é igual a duas vezes a freqüência
do sinal : não é possível a sua reprodução
pois o sinal PAM vale zero. ( obs.: se houvesse defasamento dos pontos
de amostragem, haveria sinal PAM, porem com amplitude errada, a não
ser que por coincidência os pontos caíssem nos picos da senoide,
donde a necessidade do "maior
que o dobro" no Teorema de Nyquist.
Em baixo, a freqüência de amostragem é menor que
o dobro da freqüência do sinal : a quantidade de amostras é
insuficiente e o sinal reproduzido estará errado, em vermelho na
figura. Este erro é causado pelo fenômeno de aliasing.
Vejamos agora qual é o espectro do sinal PAM.
O sinal de amostragem (que atua na chave) é constituído
de impulsos com a freqüência de amostragem fam, também
chamado função pente (ou fução amostra). O
espectro deste sinal contem raias de mesmo nível e freqüência
múltiplas inteiras de fam, ou seja, 0 Hz (componente continua),
fam, 2fam, 3fam, 4fam ... (até o infinito se a duração
do impulso for nula...).
O sinal PAM terá portanto estas mesmas raias, porem com as bandas
laterais criadas pela modulação em
amplitude, como mostra a figura seguinte, onde fa=fam e é maior
que 2 fsinal para não ter aliasing :
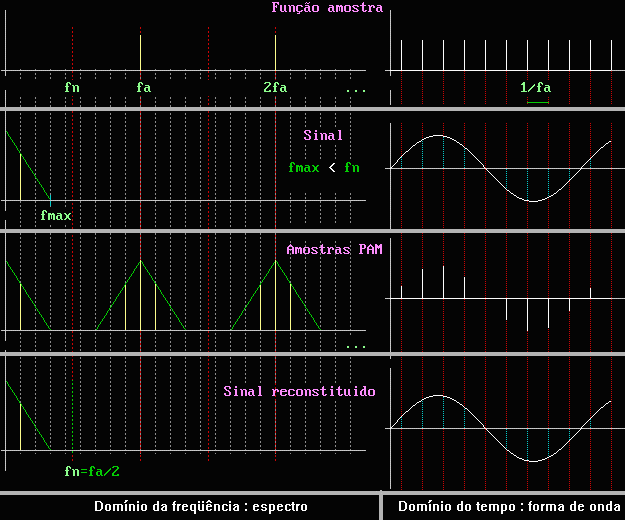 Na figura acima podemos fazer um dedução importante : para
reconstituir o sinal PAM no sinal analógico
original, basta passar o sinal PAM por um filtro passa baixo. Mostraremos
ainda que para que o sinal seja perfeitamente reproduzido, a freqüência
de corte deste filtro passa baixo deve ser exatamente igual a fn = freqüência
de Nyquist, que é igual a metade da freqüência de
amostragem ( para não haver interferência intersimbólica
IIS ).
Na figura acima podemos fazer um dedução importante : para
reconstituir o sinal PAM no sinal analógico
original, basta passar o sinal PAM por um filtro passa baixo. Mostraremos
ainda que para que o sinal seja perfeitamente reproduzido, a freqüência
de corte deste filtro passa baixo deve ser exatamente igual a fn = freqüência
de Nyquist, que é igual a metade da freqüência de
amostragem ( para não haver interferência intersimbólica
IIS ).
Para efeitos didáticos, a envoltória do espectro do sinal
a ser amostrado é representada simbolicamente pela hipotenusa de
um triângulo, em verde, e no caso, o sinal é uma senoide.
Qualquer que fosse o sinal, por mais complexa a sua forma de onda e espectro,
desde que limitado em fn, a reconstituição seria perfeita,
usando o citado filtro.
Aliasing :
Vejamos agora o que acontece quando não há filtro anti-aliasing
e o espectro do sinal tem freqüência máxima maior que
fn :
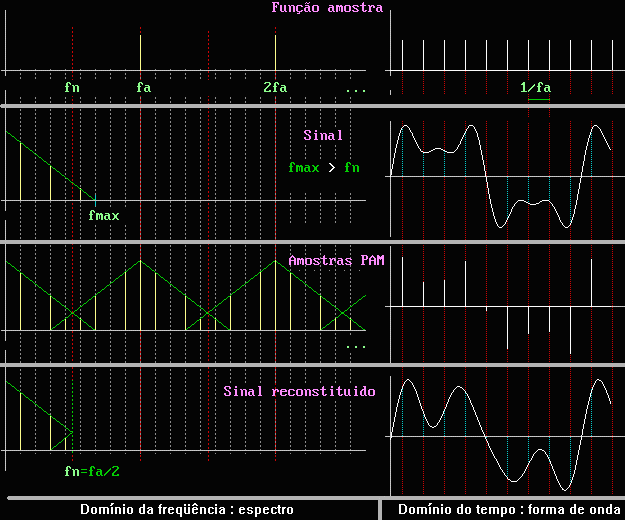 Podemos agora observar como ocorre o efeito de aliasing, que nada
mais é do que a superposição dos espectros
de cada raia mfam, por falta de espaço. Na restituição
do sinal pelo filtro passa baixo com freqüência de corte fn,
a parte do espectro original acima de fn (no caso a ponta do triângulo)
aparece como se tivesse sido dobrada em torno de fn e invertida espectralmente,
ou seja, freqüências mais altas passam a ser menores. O sinal
indesejável de aliasing que aparece na reprodução
é uma réplica do sinal original fo, porém
com freqüência errada e igual a fa-fo.
Podemos agora observar como ocorre o efeito de aliasing, que nada
mais é do que a superposição dos espectros
de cada raia mfam, por falta de espaço. Na restituição
do sinal pelo filtro passa baixo com freqüência de corte fn,
a parte do espectro original acima de fn (no caso a ponta do triângulo)
aparece como se tivesse sido dobrada em torno de fn e invertida espectralmente,
ou seja, freqüências mais altas passam a ser menores. O sinal
indesejável de aliasing que aparece na reprodução
é uma réplica do sinal original fo, porém
com freqüência errada e igual a fa-fo.
Osbserve como a forma de onda do sinal restituído é deformada
em relação ao original.
Nota : Um termo correto em português para aliasing seria freqüências
réplicas, mas como é pouco difundido, prefiro usar o
termo inglês aliasing.
Matematicamente, as freqüência réplicas ocorrem para
qualquer sinal com freqüência fs maior que fn,
e seu valor na reprodução é igual ao valor absoluto
da diferença entre a freqüência do sinal fs
e m vezes a freqüência de amostragem fam, onde
m é um inteiro tal que 0 < |(fs-m.fam)| < fam /
2.
Veja também um ótimo exemplo
(sem filtro anti-aliasing) onde a freqüência máxima do
sinal é tão alta em relação a taxa de amostragem,
a ponto de ocorrerem duas dobras do espectro, sendo a primeira em fn,
raias com número vermelho, e a segunda dobra em 2fn, o que
a faz cair em zero Hz, com as raias com números em magenta.
As duas ultimas figuras acima foram feitas com o programa RZ2,
onde é possível interagir em diversos parâmetros e
ver o resultado nos espectros e na forma de onda do sinal restituído.
 Índice
Índice





![]() Índice
Índice