O efeito do atrito com a atmosfera
sobre a velocidade de um satélite.
Por PY4ZBZ em 07-02-2006. rev. 19-09-2015
Contrariamente ao que a grande maioria acha, o efeito do atrito de um satélite com a atmosfera causa um AUMENTO da sua velocidade !
Eu também pensava que a velocidade diminuía, até estudar os livros de física citados na bibliografia. Os meus alunos também achavam o mesmo. E vejam o resultado da enquête sobre o tema, feita num grupo de pessoas, o SatFM, que lidam com satélites para radio amadores, portanto não totalmente leigas no assunto. Obrigado a todos pela participação!:
Atenção: todos os parâmetros como a, m, G, M, etc... usados nesse texto, estão definidos aqui.
De acordo com as leis de Newton, um satélite se mantém em órbita porque as duas forças que atuam nele são iguais: a força de atração gravitacional da terra Fa = GMm/a2 , e a força centrípeta Fc = mv2/a (m é a massa do satélite e v a sua velocidade). Desta igualdade podemos então deduzir qual é a velocidade exata que um satélite precisa ter para permanecer em órbita: v = ( GM/a)1/2 . Observe que esta velocidade v independe da massa m do satélite, o que permite que astronautas (com massa muito menor que a ISS, "passeiam" junto dela, com a mesma velocidade !. E observe também que quando mais baixa a altura da órbita (a menor), maior será esta velocidade ! (veja um exemplo aqui)
Isto é verdade se o satélite estiver totalmente fora da atmosfera, como no caso da lua ou por exemplo de satélites GEO, geoestacionários, que estão bem altos (35786 km) e praticamente totalmente fora da atmosfera ! Estes últimos sofrem com outros efeitos, como o fato da terra não ser bem esférica, vento solar, efeito da presença da lua e outros. Nas equações anteriores, GM/a2 é a aceleração gravitacional da terra, e v2/a é a aceleração centrípeta. A primeira é proporcional a constante gravitacional G e a massa da terra M, e inversamente proporcional ao quadrado da distancia a do satélite ao centro da terra. A segunda é proporcional ao quadrado da velocidade v do satélite e inversamente proporcional a esta distancia a.
O efeito do atrito com a atmosfera de objetos como automóveis, bicicletas, aviões, etc... é muito bem conhecido e totalmente comprovado: diminui a sua velocidade ! (se não tiver uma força suplementar para vencer esse atrito, ou qualquer outro atrito como rolamentos, etc...) ! E isso leva as pessoas a acharem que acontece o mesmo com satélites da terra. Mas a mecânica da órbita de um satélite é um pouco mais complexa do que parece !
Vejamos então o que acontece aos satélites em órbita da terra, principalmente os de órbita mais baixa, como os LEO (Low Earth Orbit), onde o efeito do atrito com a atmosfera (drag) não é desprezível. Porque mesmo em alturas acima de 300 km, a atmosfera ainda existe, mesmo que muito tênue (por exemplo: a 320 km, pressão atmosférica de 10e-17 mb e a 480 km, 10e-27 mb). Por isso mesmo a maioria dos satélites está em órbitas bem mais altas, para terem uma vida útil maior e não precisarem de "re-boosts". A ISS está numa órbita baixa pois o ônibus espacial não chega mais alto, ficaria muito mais caro, e outros motivos !
Vamos primeiro mostrar fatos reais, que acontecem com um satélite LEO bem conhecido: a ISS. A figura seguinte mostra muito bem o efeito do atrito da atmosfera sobre a altura da ISS, e que precisa de vez em quando receber a ajuda de um motor de foguete (geralmente da nave de reabastecimento) para compensar a diminuição da altura causada pelo atrito da atmosfera. Sem estas ajudas para elevar a altura ("re-boosts"), a ISS cairia cada vez mais depressa e acabaria se queimando na atmosfera que é cada vez mais densa em alturas menores :
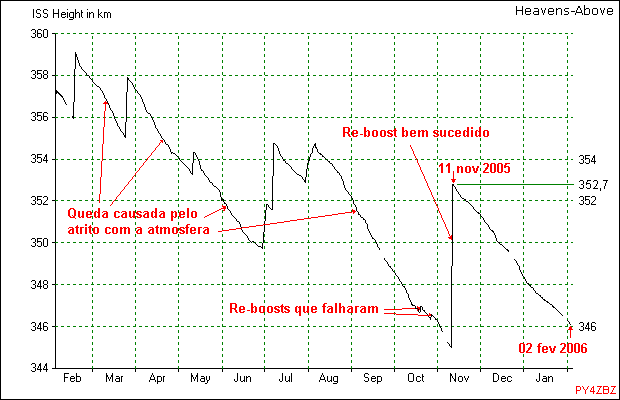
Na figura acima, (do site Heavens-Above), as anotações em vermelho são minhas. Vamos analisar a variação da altura em função do tempo, entre os dias 11 nov 2005 e 02 fev 2006, período durante o qual não foi ligado nenhum motor. É fácil verificar que a altura mudou de 352,7 km para 346 km, ou seja, caiu 6,7 km neste período de 83 dias. Como a órbita da ISS é ligeiramente elíptica, a altura no gráfico se refere a altura média (entre o apogeu e o perigeu), e corresponde ao semi-eixo maior "a" da órbita menos o raio da terra. Por exemplo, 346 km em 02/02/2006, com apogeu de 352 km e perigeu de 340 km, para uma excentricidade de apenas 0,009122. (O circulo tem excentricidade zero).
Vemos claramente o efeito do atrito sobre a altura da órbita, causando uma queda. Obs.: esta queda não é perfeitamente linear, devido a pequenas variações da pressão atmosférica causadas principalmente pelas variações da atividade solar, entre outros fatores.
Mas qual é o efeito do atrito sobre a VELOCIDADE do satélite ?
Vamos fazer alguns cálculos baseados nos precisos dados keplerianos da ISS em varias datas, mostrados na figura seguinte:
O dado kepleriano que permite deduzir a velocidade do satélite (e também o semi-eixo maior da sua órbita e o seu período) é o "movimento médio " = N0 que nada mais é que o numero de revoluções do satélite em torno da terra em um dia. Por isso mesmo, estes 3 dados (velocidade, semi-eixo maior e período) não constam nos keplerianos, pois seriam redundantes !. Os 5 dígitos seguintes ao N0 correspondem ao numero da órbita da época dos dados e o ultimo digito é um checksum da linha 2 inteira. Por exemplo, os dados de 02/02/2006 foram medidos durante a órbita #41200, num instante exato informado pelo terceiro dado da linha 1, no caso 06033.92501278, que significa 2006 + 33,92501278 dias ou 02/02/2006 as 22:12:01,1.
O período P da órbita (tempo que o satélite leva para dar uma volta), a velocidade v do satélite e o semi-eixo maior a da órbita são obtidos do movimento médio N0 pelas formulas seguintes (onde para facilitar, eu substituí as constantes 2 p ,G ,M pelo seu valor):
Período: P = 86400 / N0 ( P em segundos). (86400 s = 1 dia)
Velocidade: v = ( 2 p G M / P )1/3
ou v = ( 2504484 / P )1/3 = ( 28,987083 N0 )1/3 (para velocidade v em km/s)
Semi-eixo maior: a = ( P2 G M / 4 p2 )1/3
ou a = (10096,68 P2 )1/3 = ( 75371312332800 / N02 )1/3 (para semi-eixo maior a em km)
A tabela seguinte mostra o resultados dos cálculos para o período de tempo mencionado:
| Data | Hora (h:m:s) | N0 | P (s) | P (h:m:s ) | a (km) | v (km/s) |
| 11-11-2005 | 00:47:13 UTC | 15,72085625 | 5495,88 | 1:31:35,88 | 6731,07 | 7,69532 |
| 02-02-2006 | 22:12:01 UTC | 15,74434970 | 5487,68 | 1:31:27,67 | 6724,37 | 7,69915 |
| Variação: | +2013:24:48 | +0,02349345 | - 8,2 s | - 8,2 s | - 6,7 km | + 3,83 m/s |
Pode ser visto que nesse período de 83 dias+21:24:48 a altura caiu 6,7 km, confirmando o gráfico da altura acima. E pode ser visto que a velocidade AUMENTOU em 3,83 m/s ! Tanto que o período diminuiu em 8,2 segundos. Na lista de keplerianos acima, é perfeitamente visível o AUMENTO do movimento médio N0, que é proporcional ao aumento da velocidade do satélite, mesmo dia a dia !
Portanto:
O efeito do atrito da atmosfera AUMENTA a VELOCIDADE do satélite, além de diminuir a sua altura.
Esta é uma conclusão baseada em DADOS reais. A seguir, mostrarei a física deste fato, com a grande ajuda do Nobel de física, L.Landau.
Um satélite em órbita tem uma energia total E que é a soma da energia cinética K com a energia potencial gravitacional U.
Energia cinética: K = mv2/2 = GMm/2a (é proporcional ao quadrado da velocidade v do satélite)
Energia potencial gravitacional: U = -GMm/a = - 2K (é negativa pois é nula para a=infinito)
Energia total: E = K+U = GMm/2a - GMm/a = - GMm/2a = - K
É interessante notar que a energia total é igual a energia cinética com sinal trocado.
O atrito com a atmosfera causa diminuição da energia total E do satélite, sendo que a energia perdida na diminuição é transformada em calor. Como a energia E tem sinal negativo, ela sofre um aumento em valor absoluto. Portanto, o semi-eixo maior a DIMINUI (pois GMm é constante). Pela formulas acima, esta diminuição de a causa um aumento da energia cinética K e uma diminuição da energia potencial U. Como a energia cinética K é inversamente proporcional ao dobro de a (2a), esta varia duas vezes mais que a energia potencial, que é inversamente proporcional a a. Portanto, a soma E das duas continua sempre negativa. Então,se a energia cinética K aumenta, e como K = mv2/2, e sendo m constante (m = massa do satélite), a velocidade só pode aumentar também, pois v = (2K/m)1/2.
As fotos seguintes mostram o SuitSat (um velho traje espacial...) se afastando da ISS. Na foto colorida, é possível ver a antena de um quarto de onda para 145,99 MHz, no capacete:


Não posso deixar de citar este ótimo exemplo, bem divulgado e filmado, que foi o lançamento do SuitSat em 03-02-2006 as 23:03 UTC, durante um "passeio" dos astronautas da ISS. Um dos astronautas, com a força do braço, imprimiu ao SuitSat uma velocidade da ordem de 0,5 m/s, na direção oposta ao movimento da ISS, ou seja, para trás em relação ao movimento da ISS na sua órbita. Então a velocidade do SuitSat ficou menor que da ISS, como se tivesse sido "freado" pelo astronauta, o que tem o mesmo efeito de ter sido freado pela atmosfera !.(Esta operação é chamada de "deorbit" e é a mesma técnica usada para fazer a reentrada do ônibus espacial, com a diferença de que não é feita no braço !...mas com os motores OMS do ônibus, que nessa ocasião é virado de trás pra frente, para que os jatos dos motores estejam na direção do movimento e causem a diminuição instantânea da velocidade e altura, quando acionados).
Portanto, o SuitSat partiu da mesma órbita da ISS, mas com uma velocidade total 0,5 m/s menor que a ISS, que no momento era da ordem de 7700 m/s. Com esta menor velocidade, a força centrípeta Fc fica menor que a gravitacional Fa, o que causa uma queda da altura do SuitSat, que continua ficando cada vez mais para trás da ISS, como pode ser visto nas filmagens. Mas alguns minutos depois, e a uns 300 metros atrás da ISS, e com a altura diminuindo, acontece um aumento gradual da velocidade do SuitSat (pelo motivos explicados anteriormente). Esse aumento de velocidade é tal que o SuitSat acaba ultrapassando a ISS, um pouco abaixo dela. Tanto que apos 1 órbita (ou pouco mais de 91 minutos), o SuitSat já tem velocidade da ordem de 1m/s maior que a ISS e já está cerca de 5 km na frente da ISS e aproximadamente 800 metros abaixo! Não podia ter exemplo melhor para ilustrar esse artigo. E qualquer um, com um pouco de conhecimento, e de posse dos keplerianos adequados, pode verificar todos estes dados usando por exemplo o ótimo programa Orbitron, o que fica mais fácil que usar as formulas acima, mas que fornecem os mesmos resultados.
Observação: esta é a única forma correta de descartar um objeto da ISS: jogando-o para TRÁS. Jogando-o para frente, ou para baixo ou para cima (em relação a terra), ou para os lados, terá como consequência desastrosa o retorno do objeto para as proximidades da ISS, após um certo tempo, podendo se chocar com ela, como quase aconteceu com uma ferramenta jogada para baixo (jogada sim, porque não "cai" sozinha em órbita !) durante um passeio em 2001. Veja detalhes aqui.
Em 03-08-2011 tivemos mais um exemplo de como se "descarta" um objeto da ISS. Um cosmonauta lançou manualmente o ARISSat para trás, durante um passeio espacial, como mostram as figuras seguintes da NASA. Na primeira consta claramente: CONTRA O VETOR VELOCIDADE (ou seja, para trás) com uma velocidade de 0,5 a 1 m/s com a força dos braços ! e dentro de um cone de tolerância com 30 graus. Portanto, foi lançado com uma velocidade da ordem de 1 m/s MENOR que a ISS ! Mas um dia depois, o ARISSat já estava 2 km abaixo da ISS e 7 km na frente dela, e com velocidade 1 m/s MAIOR !

Outro exemplo pertinente é o lançamento pela ISS do cubesat brasileiro AESP-14. Veja aqui.
CONCLUSÃO FINAL:
Contrariamente ao que a grande maioria acha, o efeito do atrito de um satélite com a atmosfera causa um AUMENTO da sua velocidade !
Tudo que foi dito acima é valido para alturas do satélite acima de uns 250 km, dependendo da relação área/massa do satélite.
Abaixo de 200 km de altura, a atmosfera fica tão densa que o atrito passa a causar aumento da temperatura do satélite com uma equivalente perda de sua energia cinética, o que então reduz a sua velocidade e a sua altura, e cada vez mais rapidamente, como pode ser visto no exemplo da figura seguinte, que mostra dados reais por mim levantados do ARISSAT (mais detalhes aqui). O aumento de temperatura abaixo de uns 150 km é tanto que o satélite acaba se desintegrando e queimando na atmosfera. Em grandes satélites, como o ônibus espacial ou terceiros estágios de foguetes, algumas partes maiores podem atingir a terra sem queimar totalmente.

Bibliografia e links:
La physique à la portée de tous. de L.Landau e A.Kitaïgorodski (Éditions MIR, Moscou)
Fundamentals of Physics Extended. de Halliday, Resnick e Walker (J. Wiley & Sons, Inc.)
Satellite Orbit Paradox: A General View. de Leon Blitzer, University of Arizona
Satellite Orbital Decay Calculations THE AUSTRALIAN SPACE WEATHER AGENCY
Introduction to Astronautics Vladislaw Pustõnski
.