 Informationen über Kepler-Elemente
Informationen über Kepler-Elemente Informationen über Kepler-Elemente
Informationen über Kepler-Elemente
© DC9ZP 2005
Grundsätze
Zur Bahnbestimmung eines Satelliten benötigt man sechs voneinander unabhängige Parameter, die Keplerelemente. Grundaussagen über den Ursprung und Genauigkeit dieser essentiellen Daten werden für den Satellitennutzer zusammengefasst. Die mathematische Ableitung der Keplerelemente ist hier nicht das Thema, kann bei Interesse aber in [3] nachgelesen werden.
Seit dem Beginn der Raumfahrt versuchen die USA die Raketenstarts aller Nationen zu registrieren. Grund war die im „Kalten Krieg“ gewonnene Erkenntnis, dass sich die Starts von Satellitenträgern oder Atomraketen in der Anfangsphase voneinander nicht unterscheiden. Außerdem sollten gestartete Satelliten - eigene oder fremde - registriert und vermessen werden. Diese Aufgabe dient primär der nationalen Sicherheit der USA und wurde seinerzeit NORAD übertragen.
NORAD ist die Abkürzung für "North American Aerospace Defense Command", es ist eine dem US-Pentagon unterstellte Kommandobehörde in Chayenne Mountain, Colorado.
Im Laufe der Jahre entwickelte sich aus dem militärischen Beobachtungsdienst ein Service für alle Satellitennutzer. Im NORAD Objektkatalog sind nach 48 Jahren Raumfahrt mehr als 28000 Satelliten, Raketenteile und Weltraummüll (Debris) enthalten.
Auch wenn die Behörde mittlerweile in „United States Air Force Space Command“ (USAFSC) umbenannt wurde, bleibt NORAD als Markenzeichen für die Lieferung von Satellitendaten im Sprachgebrauch bestehen. Das USAFSC ermittelt pro Tag ca. 8000 Keplerelemente für Satelliten und gibt diese an verschiedene, akkreditierte Bedarfsträger heraus.
Alle Keplerelemente, die im Amateurfunk genutzt werden, gehen auf die NORAD-Berechnungen zurück. Das sogenannte AMSAT-Format (Bild 1) ist eine durch Umwandlung aus dem NORAD-Datensatz entstandene, speziell auf die Bedürfnisse der Funkamateure zugeschnittene Art der Darstellung der Keplerelemente.
Sicherheit und Satellitendaten
Bis zum 31.03.2005 war es möglich, die von der NORAD über die NASA gelieferten Daten frei herunterzuladen und beliebig weiter zu verbreiten. So konnten auch die AMSAT-Organisationen der verschiedenen Länder einen leistungsfähigen Keplerupdateservice bieten. Die Genehmigung ist bis 2007 zwar verlängert worden, das künftige Verfahren ist aber noch ungewiss.
Aufgrund der aktuellen Gesetzgebung der USA, die Ausfluss eines geänderten Sicherheitsdenkens sind, wird die Nutzung von Keplerdaten weigehend von der Registrierung jedes einzelnen Nutzers abhängig gemacht. Dazu muss man sich auf der Internetseite[1] des USAFSC, die sich offiziell als Regierungsseite bezeichnet, mit voller Anschrift, Telefonnummer etc. registrieren lassen. Das ist unproblematisch für Amateurfunker, die sich nicht scheuen, ihre persönlichen Daten der US-AIRFORCE und damit der Regierung der USA zu überlassen. Man kreuzt im großen Fragenkatalog dazu „HAM RADIO Operator“ an. Die Weiterverbreitung der Keplerdaten ist jetzt verboten, ein entsprechender Disclaimer weist daraufhin. Wer es dennoch macht, wird von der Lieferung dauernd ausgeschlossen. Es wird auch darauf hingewiesen, dass die Aktivitäten der Nutzer nach dem Einloggen überwacht und gespeichert werden.
Datenformate

Bild 1: Keplerdatendatensatz von AO-40 im AMSAT-Format

Bild
2: Keplerdatensatz im Two-Line-Format mit dem Satellitenbezeichner als
dritte Zeile
Bild 3 zeigt die Systematik. Wie man sieht, enthält das Two-Line-Format einige Daten mehr als die AMSAT-Version. Die für die Satellitenbahnberechnung signifikanten Differenzen bestehen aus dem Feld Decay rate - im NORAD-Satz als „First Time Derivation of Mean Motion“ ( Erste Ableitung der säkularen Änderung der Mean Motion) bezeichnet und dem nur im NORAD-Original enthaltenen Feld „Bstar Drag Term“.
Die Decay rate (übersetzt: Verzögerungsrate) ist kein eigenständiges Bahnelement wie Inklination, Ra of node, oder Epoch time[3] etc., sondern ein fiktiver Wert, der ausdrückt, um welchen Betrag sich die Mean Motion des Satelliten aufgrund des Luftwiderstandes der Restatmosphäre und anderer Einflüsse täglich ändert. Die Mean Motion (übersetzt: mittlere Bewegung) ist die mittlere Anzahl der Erdumkreisungen eines ungestörten Satelliten in 24 Stunden.
Die Bezeichnung Decay rate anstelle des ursprünglichen NORAD-Terminus, ist also eine Erfindung der AMSAT, sie gilt nur für das relativ einfache NORAD-Rechenmodell SGP - eine Abkürzung von „Simplified Generalized Propagation Model“, dass für Amateurfunkzwecke aber zu guter Genauigkeit führt. Für höhere Ansprüche - die über das hinausgehen, was für dew Amateurfunk notwendig ist - hat NORAD zwei weitere mathematische Modelle entwickelt (SGP4/SDP4 und SGP8/SDP8). Für diese Modelle wird der schon angesprochene - in den TLE enthaltenen Drag-Koeffizient B* (B-Star) genannt - verwendet. Dieser leitet sich aus einem spezifischen ballistischen Koeffezienten und dem Durchmesser des Satelliten im Verhältnis zur Masse ab. Die Verarbeitung dieses Koeffizienten in Satellitenprogrammen ist komplex und erfolgt daher nur in den Profi-Modellen der NORAD.
Daraus folgt, dass Satellitenprogramme, die mit AMSAT-Datensätzen, also mit Decay rate rechnen, die höhere Genauigkeit nicht erreichen können. Programme, die beide Formate von Keplerelementen lesen können, können das in der Regel auch nicht, da der AMSAT-Datensatz der kleinste gemeinsame Nenner für die Berechnung ist.
Das NORAD-Modell SGP4 ist für Satelliten auf niedrigen Flugbahnen mit einer Umlaufzeit von < 200 Minuten anzuwenden, während das SDP4 Modell (D = Deep Space) z.B. für AO-40/P3-E zutrifft, hier hat der B* u.a. auch Einflüsse der Schwerkraft von Sonne und Mond auf den Satelliten sowie den Strahlungsdruck der Sonne zu repräsentieren. Die Restatmosphäre spielt bei solchen Satellitenbahnen keine große Rolle mehr. Die Modelle SGP4/SDP4 und SGP8/SDP8 sind in der Genauigkeit identisch, rechnen aber nach unterschiedlichen mathematischen Verfahren[3].
Einzelheiten zur Einbeziehung des B* können für mathematisch Interessierte in [4] nachvollzogen werden, in [4] sind auch FORTRAN-Routinen zur Berechnung enthalten. An gleicher Stelle gibt es auch von Colonel Dr. Kelso die SGP4/SDP4 Routinen in Turbo-Pascal übersetzt. Die Implementierung für eigene Programme ist aber wegen der Unübersichtlichkeit der Original Fortran-Routinen und der diesem Konzept folgenden Pascal-Struktur, nicht ganz einfach und daher nichts für Programmieranfänger.
Für die Genauigkeit der Keplerelemente zeichnet zwar die herausgebende Stelle verantwortlich, es gibt aber keine Garantie für den Endverbraucher, dass die NORAD-Daten in sich stimmig sind. Die vier Stellen nach dem Komma bei Winkelangaben oder die vielen Stellen der numerischen Werte, resultieren aus Hochrechnungen und sagen nichts über die absolute Genauigkeit aus.
Die Art der Bestimmung der Elemente ist je nach Satellit unterschiedlich. Während für einige Satelliten zur Verifizierung der Keplerelemente die Flugbahn mit einem RADAR-Gerät oder durch optische Verfahren vermessen wird, werden für die Mehrzahl der Satelliten die Daten nur mathematisch hochgerechnet. Das bedeutet aber nicht, dass solche Elemente a priori ungenauer sind.
Ein neuer Datensatz wird durch die NORAD herausgegeben, wenn ein Positionsfehler 5000 Meter überschreitet, das entspricht bei einer Flughöhe von 18000 km etwa einem Fehler von einer Winkelminute in der Richtung, vom QTH der Bodenstation aus gesehen.
Die veröffentlichten Bahnelemente sind sog. mittlere Elemente, sie gelten also für eine mittlere Flugbahn und sind exakt auf das NORAD SGP4/SDP4-Modell[4] abgestimmt. Die tatsächliche Flugbahn - sog. oskulierende Ellipse - weicht von der mittleren ab, wird aber aus den Keplerelementen im SGP4/8-Modell durch aufwändige Verfahren berechnet[3]. Die Konvertierung der NORAD-Keplerelemente in ein anderes Format und das nachfolgende Berechnen von Satelliten mit Programmen, die nicht nach den NORAD-Spezifikationen rechnen, führen damit zu Fehlern in der Ortsbestimmung und der Höhe des Satelliten, die statistisch nicht vorhersehbar sind.
Der typische Lagefehler des NORAD SGP4/SDP4 -Modells ist nicht höher als 1 km, das entspricht einem Richtungsfehler unter einer Winkelminute bei einer Flughöhe von 700 km. Diese Lagefehler werden durch kurzperiodische Störungen der Bahnelemente verursacht, die sich innerhalb eines Orbits wieder aufheben. Die Berechnung und Berücksichtigung dieser kurzperiodischen Störungen wird im SGP4/8-Modell nur bis zu einer gewissen Stufe durchgeführt.
Wichtiger als die absolute Genauigkeit der Bahnelemente , ist deren Konsistenz. Konsistenz bedeutet in diesem Zusammenhang die Eigenschaft, wie sich ein bestimmter Keplerdatensatz zu seinem Vorgänger und Nachfolger verhält. Man kann das mit genauen Satellitenprogrammen[3] nachvollziehen, indem man einen bestimmten Satelliten auswählt,
die Daten für einen festgelegten Zeitpunkt in der Zukunft berechnet und dann die Berechnung mit dem Vorgänger-Keplerdatensatz für den gleichen Zeitpunkt wiederholt. Hat man das geschafft, dann wird die gleiche Rechnung mit dem Nachfolger-Keplerdatensatz gemacht. Natürlich darf zwischen den einzelnen Schritten die Dokumentation nicht fehlen
( Bildschirmausdruck oder Dateifunktion).
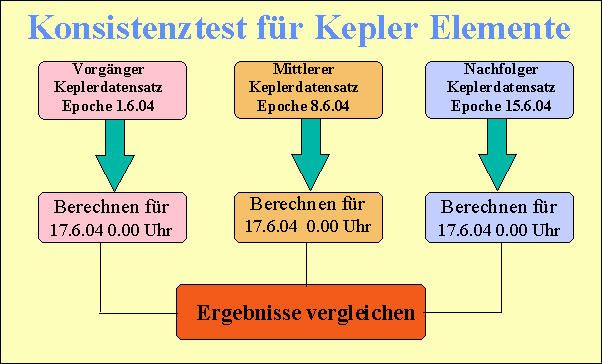
Dann vergleicht man die Daten - insbesondere die Sub-Satellitenpunkte, die Mittlere Anomalie und die Satellitenhöhen - miteinander, kleine Abweichungen sind normal. Grobe Abweichungen deuten auf eine mangelhafte Konsistenz der Keplerelemente hin, für diesen Satelliten wären die Ergebnisse in Zukunft mit Skepsis zu betrachten. Zur Vorsicht wiederholt man in solchen Fällen die Berechnung mit weiteren Keplerdatensätzen. Bild 4 zeigt das prinzipielle Vorgehen.
Wenn man mit dem einfachen SGP-Modell, also mit der AMSAT-Version der NORAD-Daten rechnet, dann ist die Nutzung der relativ ungenauen Decay rate zwangsläufig. Hier lässt mit Eigenmitteln aber einiges verbessern.
Decay rate prüfen
Die Decay Rate aus dem AMSAT-Datensatz lässt sich auf Genauigkeit dadurch prüfen, indem man zwei verschiedene Keplerdatensätze, die ca. 10-14 Tage auseinander liegen, vergleicht und dann einen mittleren Wert berechnet:
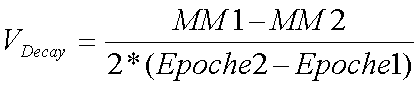
Dabei sind MM1/Epoche1 die Mean Motion/Epoch time des ersten und MM2/Epoche2 des zweiten Keplerdatensatzes. Man erhält dann den tatsächlichen Wert der Decay rate, der in der Regel erheblich von dem abweicht, was in den AMSAT-Keplerdatensätzen ausgeworfen ist. Hierbei zeigt sich dann deutlich, dass die Decay rate ein Koeffizient für verschiedene Einflüsse ist, die in der Summe mehr geschätzt als berechnet werden können. Immerhin, wenn man diese Methode öfter anwendet, ergibt sich im Laufe der Zeit ein Decay-Profil für den jeweiligen Satelliten, das genauer ist als die Decay rate im Keplerdatensatz. Bei der Anwendung dieser Methode, muss man darauf achten, dass zwischen den zu messenden Keplerdatensätzen nicht gerade eine gravierende Änderung der Flugbahn des jeweiligen Satelliten liegt, denn sonst erreicht die berechnete mittlere Decay rate leicht astronomische Werte; also nicht für die ISS oder die Space Shuttles anwenden, da diese von der Crew nachgesteuert werden.
Zur Nutzung der Decay rate sind einige Grundsätze zu
beachten
· Die Decay rate ist von allen Angaben im Keplerdatensatz sicherlich die ungenaueste, sie ist nur ein hochgerechneter Koeffizient aus einer Summe verschiedener Einflüsse und man kann nicht aUSAFSChließen, dass sie sich schnell ändert. Längere Vorhersagen mit einer bestimmten Decay rate sind daher mit Vorsicht zu betrachten, es sei denn, dass ein bestimmter Satellit über einen längeren Zeitraum immer die annähernd gleichen Werte aufweist.
· Die rechnerische Berücksichtigung der Decay rate ist kein Ersatz für einen frischen Keplerdatensatz. Der neue Satz führt auf jeden Fall zu genaueren Ergebnissen als ein veralteter mit halbwegs genauer Decay. Im Zweifel die Decay rate im Keplerdatensatz auf 0.00 setzen.
Insgesamt gesehen, ist die regelmäßige Erneuerung der Keplerdaten für die im Satellitenfunk verwendeten Programme zwingend notwendig, denn bei kurzen Zeiträumen zwischen Datum des Keplerdatensatzes und Berechnungszeitpunkt wird der Einfluss der verschiedenen Störgrößen zurückgedrängt, die Berechnung wird genauer.
Meine vergleichenden Berechnungen zwischen herkömmlichen Satellitenprogrammen die nach dem SGP-Modell unter Einbeziehung der Decay rate rechnen und den genaueren NORAD-Berechnungsmodellen SDP4/SDP8 haben ergeben, dass die Unterschiede zwischen den Ergebnissen der Programme in den ersten 14 Tagen nach der Epoche des Keplerdatensatzes relativ gering sind, dann aber erheblich ansteigen. Es zeigt sich dabei, dass die Decay rate ungenau - und der NORAD-Drag Parameter B* offensichtlich geeigneter ist, Berechnungen über längere Zeiträume zu machen.
Zum Keplerupdate sei
noch einmal anzumerken, dass es Keplerdaten nur noch nach Akkreditierung auf der
Internetseite des USAFSC[1] gibt und dass nach dem jetzigen Stand jeder Nutzer
seine Daten selbst holen muss. Ein Updateservice der AMSAT-Verbände wie in der
Vergangenheit, wird es nach den gesetzlichen Bestimmungen aus den USA nicht mehr
geben. Allerdings laufen zur Zeit noch Anstrengungen sowohl auf dem
diplomatischen Weg als auch auf dem
„kleinen Dienstweg“.
Zusammenfassend
ist festzustellen, dass die veröffentlichten Keplerelemente nur dann genau
genug sind, wenn auch die entsprechenden Modelle SGP, SGP4, SDP4 oder SGP8/SDP8
zur Berechnung verwendet werden, und dass ein Programm nicht genauer rechnen
kann als das, was die Genauigkeit der Keplerelemente hergibt. Dazu ein
treffender, wenn auch angelsächsischer Grundsatz: Garbage in = Garbage out.
Literatur/Hinweise auf Fundstellen
[1] USAFSC
:http://www.space-track.org/
[2] Weitere Einzelheiten der Bedeutung der TLE-Daten in: http://celestrak.com/NORAD/documentation/
[3] Maday, Manfred, DC9ZP, „Amateurfunksatelliten, Übersicht, Berechnung und Software“,
E-Book (PDF-Datei), Info beim Autor: dc9zp@darc.de
[4] Spacetrack Report 3 der NORAD von 1980, herunterzuladen bei: http://celestrak.com/NORAD/documentation/spacetrk.pdf
I Erklärung der verschiedenen Formate (Englisch)
1. NORAD-Two-Line Keplerian Elements
A NORAD two-line element set consists of two 69-character lines of data which can be used together with NORAD's SGP4/SDP4 orbital model to determine the position and velocity of the associated satellite. The only valid characters in a two-line element set are the numbers 0-9, the capital letters A-Z, the period, the space, and the plus and minus signs - no other characters are valid. Of course, not all valid characters can be used in all columns within the element set. Figure 1 shows what type of character is valid for each column. Columns with a space or period can have no other character. Columns with an 'A'can have any number 0-9 or, in some cases, a space. Columns with an ‘A’ can have any character A-Z or a space. The column with a 'C' can only have a character representing the classification of the element set - normally either a 'U' for unclassified data or an 'S' for secret data (of course, only unclassified data are publicly available). Columns with a '+' can have either a plus sign or a space and columns with a '-' can have either a plus or minus sign.
1 NNNNNC NNNNNAAA NNNNN.NNNNNNNN +.NNNNNNNN +NNNNN-N +NNNNN-N N NNNNN
2 NNNNN NNN.NNNN NNN.NNNN NNNNNNN NNN.NNNN NNN.NNNN NN.NNNNNNNNNNNNNN
Figure 1. Two-Line Element Set Format
Further restrictions are placed upon the values in each column as the individual fields of data are defined. Tables 1 and 2 define each of the individual fields for lines 1 and 2, respectively. Many of these bear additional explanation.
|
Column |
Field |
Range |
Units |
Remarks |
|
1 |
Line Number |
1 |
- |
Identifies Line 1 |
|
2 |
blank space |
- |
- |
Invariant |
|
3 - 7 |
Catalog Number |
1 - 99999 |
- |
Sequential Sat ID |
|
8 |
Classification |
U, C, S |
- |
Always U nclassified for Publicly-released TLEs |
|
9 |
blank space |
- |
- |
Invariant |
|
10 - 17 |
International Designator |
- |
- |
cols
10 to 11 - 2-digit year
cols 12 to 14 - launch number cols 15 to 17 - piece ID |
|
18 |
blank space |
- |
- |
Invariant |
|
19 - 32 |
Epoch Time |
- |
- |
cols
19 to 20 - 2-digit year
cols 21 to 23 - day of year col 24 - decimal point cols 25 to 32 - fraction of day |
|
33 |
blank space |
- |
- |
Invariant |
|
34 - 43 |
ndot/2 |
-0.99999999 to 0.99999999 |
rev/day2 |
col
34 - sign (negative or blank)
col 35 - decimal point cols 36 to 43 - mantissa |
|
44 |
blank space |
- |
- |
Invariant |
|
45 - 52 |
nddot/6 |
- |
rev/day3 |
col
45 - sign
cols 46 to 50 - mantissa (implied leading decimal point) col 51 - tens exponent sign (always negative) col 52 - tens exponent |
|
53 |
blank space |
- |
- |
Invariant |
|
54 - 61 |
Bstar |
- |
1 / Earth Radii |
col
54 - sign
cols 55 to 59 - mantissa (implied leading decimal point) col 60 - tens exponent sign (always negative) col 61 - tens exponent |
|
62 |
blank space |
- |
- |
Invariant |
|
63 |
Ephemeris Type |
0 - 7 |
- |
Always 0 for Publicly- Released TLEs |
|
64 |
blank space |
- |
- |
Invariant |
|
65 - 68 |
Element Number |
1 - 9999 |
- |
Incremented with each update |
|
69 |
Check Sum |
0 - 9 |
- |
Modulo-10 |
Column 1 of each line of the two-line element set indicates the line number (and hence the format) for that line. The next field on each line indicates the satellite number - actually, the NORAD Catalog Number - of the object the data is for. The NORAD Catalog Number is a unique identifier assigned by NORAD for each earth-orbiting artificial satellite in their SATCAT (Satellite Catalog). For a valid two-line element set, fields 1.2 and 2.2 must be identical. As mentioned above, field 1.3 indicates the security classification of the data - all publicly available data will have a 'U' in this field to indicate unclassified data.
The next three fields - fields 1.4 through 1.6 - define the International Designator of the object. This identifier is an additional unique designation assigned by the World Data Center-A for Rockets and Satellites (WDC-A-R&S) in accordance with international treaty (1975 Convention on Registration of Objects Launched into Outer Space). The WDC-A-R&S works together with NORAD and NASA’s National Space Science Data Center (NSSDC) in maintaining this registry. Although there have been some changes in format since it was first used back in the late 1950s (see "Space Surveillance" in Satellite Times Volume 4 Number 1), the International Designator indicates the year of the launch (field 1.4 only gives the last two digits), the launch of that year (field 1.5), and the piece of that launch (field 1.6) for each object. These three fields can be left blank, but all must be present if any is. Finally, field 1.6 can be either right or left justified -the latter is preferred. As an aside, there are some significant differences between NORAD's Catalog Number and the International Designator. For example, NORAD assigns a catalog number based upon when the object was first observed, whereas the International Designator is always tied to the original launch. For example, the 81st launch of 1968 carried four payloads into orbit: OV2-5, ERS 21 and 28, and LES 6.
Together with the Titan 3C transtage rocket body, these objects were assigned International Designators 1968-081A through E and Catalog Numbers 03428 through 03431. Just this past October, however, NORAD cataloged two additional pieces associated with this launch as Catalog Numbers 25000 and 25001 - they have the International Designators 1968-081F and G.
The next two fields (fields 1.7 and 1.8) together define the reference time for the element set and are jointly referred to as the epoch. Field 1.7 is the two-digit year (more on this later) and field 1.8 is the day of that year. The epoch defines the time to which all of the time-varying fields in the element set are referenced.
While talking about the epoch, this is perhaps a good place to answer the other time-related questions. First, how is the epoch time format interpreted? This question is best answered by using an example. An epoch of 98001.00000000 corresponds to 0000 UT on 1998 January 01 -in other words, midnight between 1997 December 31 and 1998 January 01. An epoch of 98000.00000000 would actually correspond to the beginning of 1997 December 31 - strange as that might seem. Note that the epoch day starts at UT midnight (not noon) and that all times are measured mean solar rather than sidereal time units (the answer to our third question).
Apparently, US Space Command sees no need to change the two-line element set format yet since no artificial earth satellites existed prior to 1957. By their reasoning, two-digit years from 57-99 correspond to 1957-1999 and those from 00-56 correspond to 2000-2056. Therefore, there is no need to change the format for another 50 years! Unfortunately, this reasoning is severely flawed. While changing the format would involve changing large numbers of software packages to accommodate the format changes, not changing the format does not remove the need to modify this software. Instead of incorporating a format change along with the software modifications, modifications must be made now to change the epoch interpretation and later when the format is finally changed. Too bad that when Aerospace Defense Command proposed going from the old five-line to the current two-line format in November 1972 they didn’t recommend a four-digit year (they did, however, at least change from a one-digit to a two-digit year).
Field 1.9 represents the first derivative of the mean motion divided by two, in units of revolutions per day2, and field 1.10 represents the second derivative of the mean motion divided by six, in units of revolutions per day3. Together, these two fields give a second-order picture of how the mean motion is changing with time. However, these two fields are not used by the SGP4/SDP4 orbital models (only by the simpler SGP model) and, therefore, serve no real purpose.
Field 1.11 represents something called B* (BSTAR), which is an SGP4-type drag coefficient. In aerodynamic theory, every object has a ballistic coefficient, B, that is the product of its coefficient of drag, CD, and its cross-sectional area, A, divided by its mass, m.
B = CD A/m
The ballistic coefficient represents how susceptible an object is to drag -the higher the number, the more susceptible. B* is an adjusted value of B using the reference value of atmospheric density, r
B* = B r /2
B* has units of (earth radii)-1.
Fields 1.10 and 1.11 have a somewhat different format that the other fields. In particular, they use a modified exponential notation with an implied leading decimal point. This convention is inherited from FORTRAN where all such numbers range from 0 to less than 1. The first six columns of each field represent the mantissa and the last two represent the exponent. For example, the value -12345-6 corresponds to -0.12345 10-6. Each of these two fields can be blank, corresponding to a value of zero. Field 1.12 represents the ephemeris type (i.e., orbital model) used to generate the data. Spacetrack Report Number 3 suggests the following assignments: 1=SGP, 2=SGP4, 3=SDP4, 4=SGP8, 5=SDP8. However, this value is used for internal analysis only -all distributed element sets have a value of zero and are generated using the SGP4/SDP4 orbital model (as appropriate).
Field 1.13 represents the element set number. Normally, this number is incremented each time a new element set is generated. In practice, however, this doesn’t always happen. When operations switch between the primary and backup Space Control Centers, sometimes the element set numbers get out of sync, with some numbers being reused and others skipped. Unfortunately, this makes it difficult to tell if you have all the element sets for a particular object.
The last column on each line (fields 1.14 and 2.10) represents a modulo-10 checksum of the data on that line. To calculate the checksum, simply add the values of all the numbers on each line -ignoring all letters, spaces, periods, and plus signs -and assigning a value of 1 to all minus signs. The checksum is the last digit of that sum. Although this is a very simple error-checking procedure, it should catch 90 percent of all errors. However, many errors can still sneak through. To eliminate these, all data posted on the Celestial WWW site not only pass the checksum test, but must also pass both format and range-checking tests (as described in this article).
Line 2 consists primarily of mean elements calculated using the SGP4/SDP4 orbital model. The definitions for fields 2.3 through 2.8 can be seen in table 2 below. Fields 2.3, 2.4, 2.6, and 2.7 all have units of degrees and can range from 0 up to 360 degrees -field 2.3 (inclination) only goes up to 180 degrees.
The eccentricity (field 2.5) is a unitless value with an assumed leading decimal point. For example, a value of 1234567 corresponds to an eccentricity of 0.1234567. The mean motion (field 2.8) is measured in revolutions per day.
|
Column |
Field |
Range |
Units |
Remarks |
|
1 |
Line Number |
2 |
- |
Identifies Line 2 |
|
2 |
blank space |
- |
- |
Invariant |
|
3 - 7 |
Catalog Number |
1 - 99999 |
- |
Must be the Same as cols 3 - 7 for Line 1 |
|
8 |
blank space |
- |
- |
Invariant |
|
9 - 16 |
Inclination |
0.0000 to 180.0000 |
degrees |
col 12 is the decimal point |
|
17 |
blank space |
- |
- |
Invariant |
|
18 - 25 |
Right Ascension of the Ascending Node |
0.0000 to 359.9999 |
degrees |
col 21 is the decimal point |
|
26 |
blank space |
- |
- |
Invariant |
|
27 - 33 |
Eccentricity |
0000010 - 9500000 |
- |
decimal point is implied between cols 26 and 27 |
|
34 |
blank space |
- |
- |
Invariant |
|
35 - 42 |
Argument of Perigee |
0.0000 - 359.9999 |
degrees |
col 38 is the decimal point |
|
43 |
blank space |
- |
- |
Invariant |
|
44 - 51 |
Mean Anomaly |
0.0000 - 359.9999 |
degrees |
col 47 is the decimal point |
|
52 |
blank space |
- |
- |
Invariant |
|
53 - 63 |
Mean Motion |
- |
rev/day |
col 55 is the decimal point |
|
64 - 68 |
Revolution Number |
1 - 99999 |
- |
rev increments at each ascending node |
|
69 |
Check Sum |
0 - 9 |
- |
Modulo-10 |
The final field on line 2, prior to the checksum, is the rev number. Since there are several conventions for determining rev numbers, this field also bears some clarification. In NORAD’s convention, a revolution begins when the satellite is at the ascending node of its orbit and a revolution is the period between successive ascending nodes. The period from launch to the first ascending node is considered to be Rev 0 and Rev 1 begins when the first ascending node is reached. Since many element sets are generated with epochs that place the satellite near its ascending node, it is important to note whether the satellite has reached the ascending node when calculating subsequent rev numbers.
In general, any number smaller than the maximum field size can be padded with either leading spaces or leading zeros. In other words, an epoch can be represented as either 98001.12345678 or 98 1.12345678 or an inclination can be represented as 28.1234 or 028.1234. Convention uses leading zeros for fields 1.5 and 1.8 and leading spaces elsewhere, but either is valid.Obviously, there are a few limitations with the current two-line format.
First and foremost is the need for a four-digit year in fields 1.4 and 1.7. Next, there is a need for a more robust form of error checking -perhaps a 16-bit CRC. Such a checksum could be applied to both lines together, not only detecting errors within the data but also mismatched lines 1 and 2. If such changes were made, it might also be wise to increase the field size for the Catalog Number to six or seven digits to support the eventual cataloging of smaller debris.The International Designator format seems to suffice for the foreseeable future, with a four-digit year, up to 999 launches (the most we’ve had to date in any one year was 129 in 1984), and up to 13,824 pieces (the record holder today is 1994-029 with 672 pieces). Of course, the cataloging of smaller debris -which we may be unable to correlate with the original launch - still presents potential problems.
1.5 Übersetzung der Zeilenangaben
| Position |
Bezeichnung |
Bemerkung |
| 1. Zeile | ||
| 01 | Zeilennummer | Immer 1. |
| 03-07 | Satellitennummer | Nummer des Satelliten im NORAD-Katalog. |
| 08 | Klassifizierung | U = nicht als GEHEIM oder VERTRAULICH klassifiziert, also offen. |
| 10-17 | Internationaler Bezeichner | Die ersten beiden Ziffern sind das Startjahr, die nächsten 3 die laufende Nummer des Start in diesen Jahr, die letzten 3 die einzelnen Komponenten des Starts. |
| 19-20 | Epoch Jahr | Die letzten zwei Zahlen der Jahreszahl, gibt zusammen mit dem Epoch Tag den Zeitpunkt an, zu dem der Datensatz berechnet - und die dazugehörige Mittlere Anomalie gemessen wurde. |
| 21-32 | Epoch Tag | Laufender Tag im Jahr mit Bruchteil des Tages. |
| 34-43 | 1. Ableitung der Mean Motion | Zahlenwert × 2 ergibt den Wert der 1. Ableitung in Umläufen/Tag2. |
| 45-52 | 2. Ableitung der Mean Motion | Zahlenwert × 6 ergibt den Wert der 2. Ableitung in Umläufen/Tag3. |
| 54-61 | BSTAR Drag term. | Ballistischer Term, der die Reibungskräfte im SGP4-Modell und SGP8-Modell ausdrückt. |
| 63 | Ephemeridentyp | Gibt an, mit welchem Modell die Daten berechnet wurden. Nur für interne Zwecke, im Regelfall nicht benutzt und mit 0 = Modell SGP4/SDP4 gefüllt. |
| 65-68 | Element Satz Nummer | Laufende Nummer des Datensatzes, beginnt am Jahresanfang neu. |
| 69 | Prüfziffer | Ergibt sich aus der Summe aller Ziffern in der Zeile, Buchstaben, ".", "+" und " " werden mit 0 bewertet, "-" mit 1, Prüfsumme mod 10 ergibt die Prüfziffer. |
| 2. Zeile | ||
| 01 | Zeilennummer | Immer 2 |
| 03-07 | Satellitennummer | Nummer des Satelliten im NORAD-Katalog. ( Backup) |
| 09-16 | Inklination | Angabe in Grad von 0-180 |
| 18-25 | Right Ascension of the Ascending Node, RAAN. | Angabe in Grad von 0-359.9999 |
| 27-33 | Exzentrizität der Bahnellipse | Führende 0 und Dezimalpunkt fehlen, also vorsetzen. |
| 35-42 | Argument des Perigäums | Angabe in Grad von 0-359.9999 |
| 44-51 | Mittlere Anomalie | Angabe in Grad 0-359.9999. |
| 53-63 | Mean Motion ( Mittlere Bewegung/Tag) | Anzahl der mittleren Umläufe pro Tag. |
| 64-68 | Revolution Number. | Umlaufnummer von Knoten zu Knoten gerechnet |
| 69 | Prüfziffer | Wie Zeile 1 |
2. AMSAT-Format Keplerian Elements
The Radio Amateur Satellite Corporation (AMSAT) developed its own verbose Keplerian element format. This format was developed to be convenient for relay over amateur radio and for clarity. Early amateur satellite tracking was manual to some degree.
Satellite:
ISS
Catalog number: 25544
Epoch time: 00225.77853128
Element set: 954
Inclination: 51.5750 deg
RA of node: 210.9643 deg
Eccentricity: 0.0011506
Arg of perigee: 237.0618 deg
Mean anomaly: 183.7134 deg
Mean motion: 15.71169901 rev/day
Decay rate: 4.6489e-4 rev/day^2
Epoch rev: 9881
Checksum:
307
The AMSAT Keplerian format is essentially a labeled subset of the NORAD-Keplerian format. The AMSAT format does not have the TLE's International Designator, Ephemeris Type, or its nddot/6 or Bstar drag terms. The decay rate is the ndot/2 drag term (Decay rate).
The AMSAT format has a single check sum computed by adding all the Keplerian element's digits, a "+1" for each negative (-) sign, and a "+2" for each plus (+) sign. Note that the digits used for computing the check sum include all characters whether they are the orbital parameters themselves or the labels (such as the "2" in the decay units label).
Keplerelemente für Satellitenberechnungen werdenin zwei verschiedenen Formaten verbreitet. Das sog AMSAT-Format enthält die Daten in 13 Datenfeldern (Siehe Tabelle), das NORAD-2LINE-Format (auch NASA 2Line genannt) besteht aus 2 Datenzeilen und einer zusätzlichen Zeile mit dem Satellitennamen.
Beide Datensätze enthalten Prüfsummen anhand denen der "Endverbraucher" feststellen kann, ob die Daten auf den verschiedenen Übertragungswegen verfälscht wurden. Die zugrunde liegenden Algorithmen sind einfach. Die Verfahren erkennen fehlende oder falsche Zeichen, aber keine Zahlendreher. In der Regel reichen diese Mechanismen jedoch aus. Gegen vorsätzliche Manipulationen kann man sich ohnehin nicht schützen.
2. Prüfsumme der AMSAT-Datensätze
Der Algorithmus ergibt sich wie folgt :
Prüfsumme = Summe aller Zahlen, sowie der '+' und '-' Zeichen im Datensatz, mit Ausnahme des Feldes Checksum. Ein Minuszeichen als Vorzeichen oder als Trennstrich eingesetzt (-) zählt als 1, ein Pluszeichen (+) als 2. ( Siehe Tabelle).
| Zeilenbezeichnung | Werte der Elemente | Zeilensumme |
| Satellite: | AO-10 | 02 |
| Catalog number: | 14129 | 17 |
| Epoch time: | 95273.14208990 | 59 |
| Element set: | 0378 | 18 |
| Inclination: | 26.4628 deg | 28 |
| RA of node: | 245.8965 deg | 39 |
| Eccentricity: | 0.5984525 | 38 |
| Arg of perigee: | 314.0229 deg | 21 |
| Mean anomaly: | 9.9399 deg | 39 |
| Mean motion: | 2.05881672 rev/day | 39 |
| Decay rate: | -1.04e-06 rev/day^2 | 15 |
| Epoch rev: | 9246 | 21 |
| Checksum: | 336 | 336 |
Beispiel als PASCAL Prozedur :
Const Pruefsumme : Integer = 0 ;
Type str80 = STRING[80];
Procedure summe(line:str80):Integer;
var i , k, zahl : Integer;
Begin
for i := 1 to length(line) do
Begin
if line[i] = '-'then line[i] := '1'
if line[i] = '+'then line[i] := '2'
val(line[i],zahl,k);
if k = 0 then
inc(pruefsumme,zahl);
End;
End;
Der AMSAT-Keplersatz wird also Zeile für Zeile (1-12) der Prozedur bei deren Aufruf übergeben, die Summen der Zeilen stehen nach Ende der Berechnung in der als global zu deklarierenden typisierten Konstante "Pruefsumme". Danach vergleicht man das Ergebnis mit dem Zahlenwert des Feldes Checksum. Beide Zahlen müssen identisch sein.
3. Prüfsumme der NASA 2Line Datensätze
Hier findet man für jede Datenzeile eine einstellige Prüfsumme. Im Gegensatz zum AMSAT-Datensatz wird die Zeile mit der Satellitenbezeichnung nicht in das Verfahren einbezogen.

Dieser Algorithmus setzt sich wie folgt zusammen :
Prüfsumme = Summe aller Zahlenwerte und der Minuszeichen in den Datenzeilen 1 oder 2 (Nur die Stellen 1-68, also nicht die Prüfsumme selbst) und danach das Ergebnis MOD 10. MOD 10 hat als Ergebnis den Rest, der bei einer Integerdivision durch 10 entsteht. Ein Minuszeichen (-) zählt 1, ein Pluszeichen wird nicht berücksichtigt, ist also 0.
Dazu ein Beispiel als PASCAL Funktion :
Function Check2line(line:str80):Integer;
Var i , k, summe, zahl : Integer;
Begin
summe := 0;
for i := 1 to 68 do
Begin
if line[i] = '-' then line[i] := '1';
val(line[i],zahl,k);
if k = 0 then inc(summe,zahl);
end;
check2line := summe mod 10;
End;
Die Funktion gibt die Prüfsumme der übergebenen Datenzeile zurück. Das Ergebnis muss identisch mit dem Zahlenwert der letzten Stelle sein.
Fehler lassen sich im Datensatz wie folgt erkennen :
|
Eine andere Zahl im Datensatz: Prüfsumme ist <> Soll, |
|
|
Ein fehlendes Minuszeichen : Prüfsumme ist um 1 zu niedrig, |
|
|
Durch Buchstaben ersetzte Zahlen : Prüfsumme <> Soll. |
|
|
Eine fehlende Zahl die <> 0 ist : Prüfsumme ist < Soll. |
Folgende Fehler werden mit diesem Verfahren nicht erkannt :
|
Es fehlt eine 0 : Prüfsumme unverändert, da 0 nicht zählt. |
|
|
Zahlendreher mit Stellentausch wie Inklination = 28.9438 anstelle von 82.9438 : Prüfsumme unverändert. |
|
|
Durch Buchstaben ersetzte 0 wie 297.a086 anstelle 297.0086 : Prüfsumme unverändert. |
|
|
Minuszeichen an falscher Stelle wie -8.4e07 anstelle von 8.4e-07 : Prüfsumme unverändert. |
Für diese Fälle müssen daher eigene Routinen der Fehlererkennung geschrieben werden, um die Keplerdatensätze auf Plausibilität prüfen.
III Weiterführende Literatur über Kepler Elemente
[1] Bisnath, S.B. and R.B. Langley; Assessment of the GPS/MET TurboStar GPS receiver for orbit
determination of a future CSA micro/small-satellite mission ; Final report by the Department of
Geodesy and Geomatics Engineering, University of New Brunswick, Frederiction, N.B. for the
Directorate of Space Mechanics, Space Technology Branch of the Canadian Space Agency, St-
Hubert, Que. under Public Works and Government Services Canada Contract No. 9F011-5-
0651/001/XSD, July, 188 pp. (1996).
[2] Briess K., Bärwald W., Gerlich Th., Jahn H., Lura F., Studemund H .; The DLR Small Satellite
Mission BIRD ; in Röser H. P., Sandau R. Valenzuela A. (eds.): Small Satellites for Earth
Observation , Disgest of the 2
nd International Symposium of the IAA, Berlin April 12-16(1999).
[3] Escobal P. R.; Methods of Orbit Determination ; John Wiley & Sons, Inc., New York (1965).
Reprint: Krieger Publishing Company, Malabar, Florida (1976).
[4] Hajj G., Kursinski E.R., Bertiger W., Leroy, Romans L., Schofield J.T.; Sensing the
atmosphere from a low-earth orbiter tracking GPS: early results and lessons from the
GPS/MET experiment; Proceedings of the ION GPS-95, Institute of Navigation, Palm Springs,
Calif, U.S.A., 12-15, Sept., pp. 1167-1174 (1995).
[5] Herman J.; General Description of the TLEGEN Software for 2-Line Elements Generation ;
FDS-GEN-1030, Issue 1.0, DLR Oberpfaffenhofen (1998).
[6] Hoots F. R., Roehrich R. L.; Models for propagation of NORAD element sets ; Project
Spacecraft Report No. 3; Aerospace Defense Command, United States Air Force; Dec. (1980).
[7] Jochim E.F., Gill E., Montenbruck O., Kirschner M .; GPS Based Onboard and Onground
Orbit Operations for Small Satellites ; Acta Astronautica 39 , No. 9-12, 917-922 (1996).
[8] Kirschner M.; General Description of the GPS2TLE Orbit Determination Program; FDSGEN-
3030, Issue 1.0, DLR Oberpfaffenhofen (2000).
[9] Montenbruck O.; An Epoch State Filter for use with Analytical Orbit Models of Low Earth
Satellites ; Aerospace Science and Technology (2000).
[10] Montenbruck O., Gill E., Orbit Determination of the MIR Space Station using MOMSNAV GPS
Measurements ; 96-c-53, 20
th International Symposium on Space Technology and Science / 11thInternational Symposium on Space Flight Dynamics; May 19-25, 1996, Gifu, Japan (1996).
[11] Montenbruck O., Gill E.; Satellite Orbits – Models, Methods, and Applications , Springer
Verlag, Heidelberg (2000).
Bearbeitungstand dieser Seite : 25.10.06